1. 某天的最低气温是零下$3^{\circ }C$,可以记作(
-3℃
)。
答案:-3℃
解析:
零上温度用正数表示,零下温度用负数表示,所以零下$3^{\circ }C$记作$-3^{\circ }C$。
2. $3.85的100$倍是(
385
),$5个2.8$是(
14
),$4.6$的一半是(
2.3
)。
答案:385
14
2.3
解析:
1. 对于$3.85$的$100$倍,我们只需将$3.85$乘以$100$。
$3.85 × 100 = 385$
2. 对于$5$个$2.8$,我们将$2.8$乘以$5$。
$2.8 × 5 = 14$
3. 对于$4.6$的一半,我们将$4.6$除以$2$。
$4.6 ÷ 2 = 2.3$
3. $2.47×1.32$的积有(
四
)位小数;$4.8÷0.06$的商的最高位是(
十
)位。
答案:四
十
解析:
2.47有两位小数,1.32有两位小数,2+2=4,积有四位小数;4.8÷0.06=480÷6=80,商的最高位是十位。
4. 一个三位小数“四舍五入”保留两位小数后是$8.70$,这个三位小数最大是
8.704
,最小是
8.695
。
答案:8.704
8.695
5. 把$6.823$的小数点先向左移动两位,再向右移动三位是(
68.23
)。
答案:68.23
解析:
6.823小数点向左移动两位得0.06823,再向右移动三位得68.23
6. $0.37公顷=$
3700
平方米 $37千克=$
0.037
吨 $4.5平方千米=$
450
公顷
答案:3700
0.037
450
解析:
因为1公顷=10000平方米,所以0.37公顷=0.37×10000=3700平方米;因为1吨=1000千克,所以37千克=37÷1000=0.037吨;因为1平方千米=100公顷,所以4.5平方千米=4.5×100=450公顷。
7. $4个0.1和9个0.01$组成的小数是(
0.49
),这个小数写成分数是(
$\frac {49}{100}$
)。
答案:0.49
$\frac {49}{100}$
解析:
0.49;$\frac{49}{100}$
8. 在$◯$里填“$>$”“$<$”或“$=$”。
$7.2×0.9$
$<$
$7.2÷0.9$ $6.6吨$
$=$
$6600$千克
$3.75÷1.25$
$<$
$3.75×1.25$ $7.8×100$
$<$
$0.78×10000$
答案:<
=
<
<
解析:
$7.2×0.9<7.2÷0.9$;$6.6吨=6600$千克;$3.75÷1.25<3.75×1.25$;$7.8×100<0.78×10000$
9. 一个平行四边形的高是$7.5$厘米,底是$6$厘米,另一个与它面积相等的平行四边形的底是$9$厘米,高是(
5
)厘米。
答案:5
解析:
$7.5×6=45$(平方厘米)
$45÷9=5$(厘米)
5
10. 一个三角形与一个平行四边形等底等高,三角形的面积是$12$平方厘米,它们的面积和是(
36平方厘米
)。
答案:36平方厘米
解析:
因为三角形与平行四边形等底等高,平行四边形面积是三角形面积的2倍。三角形面积是12平方厘米,所以平行四边形面积为$12×2 = 24$平方厘米。它们的面积和是$12 + 24 = 36$平方厘米。
36
1. 在$8.91÷a中(a≠0)$,当$a$(
②
)$1$,所得的商大于$8.91$。
① 大于 ② 小于 ③ 等于
答案:②
解析:
一个数(0除外)除以一个小于1的数,商大于这个数。在$8.91÷a$中,要使商大于$8.91$,则$a$应小于1。
2. 一个数除以$100$后,小数点再向右移动三位,得$2.86$,原来的数是(
①
)。
① $0.286$ ② $28.6$ ③ $286$
答案:①
解析:
设原来的数是$x$。
$x÷100×1000 = 2.86$
$x×(1000÷100)=2.86$
$10x = 2.86$
$x=2.86÷10$
$x = 0.286$
①
3. 一服装厂买进$560$米蓝布,做$100$套服装只用去这批布的一半,平均每套服装用布(
②
)米。
① $5.6$ ② $2.8$ ③ $28$
答案:②
解析:
这批布的一半为:$560×\frac{1}{2}=280$(米)
平均每套服装用布:$280÷100=2.8$(米)
②
4. 做一件短袖用布$1.2$米,$25$米布最多可做(
②
)件。
① $21$ ② $20$ ③ $22$
答案:②
解析:
25÷1.2≈20.83,最多可做20件。②
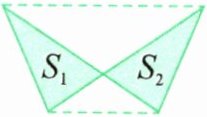
5. 如图,两条虚线互相平行,两个三角形的面积$S_{1}和S_{2}$相比,(
③
)。
① $S_{1}$大 ② $S_{2}$大 ③ 一样大
答案:③
解析:
设两条虚线间的距离为h(即三角形的高)。观察图形可知,S₁和S₂分别与中间空白三角形组成两个大三角形,这两个大三角形等底(均为两条虚线间图形的底边)等高(高均为h),所以两个大三角形面积相等。用两个大三角形面积分别减去中间空白三角形面积,可得S₁=S₂。