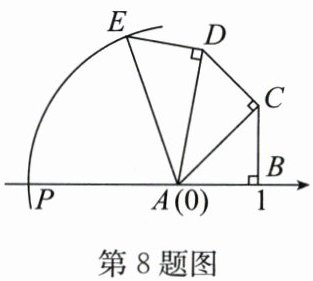
8. 如图,$ AB = BC = CD = DE $,$ \angle CBA = \angle DCA = \angle EDA = 90^{\circ} $,以点 $ A $ 为圆心,$ AE $ 长为半径画弧与数轴交于点 $ P $,点 $ A $,$ B $ 表示的数分别为 $ 0 $,$ 1 $,则点 $ P $ 表示的数为
-2
.
解析:
解:
∵点$A$表示的数为$0$,点$B$表示的数为$1$,
∴$AB = 1$。
∵$AB = BC = CD = DE$,
∴$BC = CD = DE = 1$。
在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 1^2 + 1^2 = 2$,
∴$AC = \sqrt{2}$。
在$Rt\triangle ACD$中,$AD^2 = AC^2 + CD^2 = (\sqrt{2})^2 + 1^2 = 3$,
∴$AD = \sqrt{3}$。
在$Rt\triangle ADE$中,$AE^2 = AD^2 + DE^2 = (\sqrt{3})^2 + 1^2 = 4$,
∴$AE = 2$。
∵以点$A$为圆心,$AE$长为半径画弧与数轴交于点$P$,
∴$AP = AE = 2$。
∵点$P$在点$A$左侧,
∴点$P$表示的数为$-2$。
$-2$