2025年启东中学作业本八年级数学上册苏科版宿迁专版第65页解析答案

7. (2024·宿豫期中) 如图,把一个直立的火柴盒放倒, $ AB = 5 cm $, $ BC = 2 cm $,则 $ \triangle ACD $ 的面积为

$\frac{29}{2}$

$ cm^2 $。

答案：$\frac{29}{2}$

8. 如图,火柴盒的侧面为长方形 $ ABCD $,其中 $ CD = a $, $ AD = b $, $ AC = c $。把直立的火柴盒放倒,侧面 $ ABCD $ 旋转至长方形 $ AB'C'D' $ 处。
(1) $ S_{\triangle ADC} = $

$\frac{1}{2}ab$

, $ S_{\triangle AB'C'} = $

$\frac{1}{2}ab$

, $ S_{\triangle ACC'} = $

$\frac{1}{2}c^{2}$

, $ S_{四边形CDB'C'} = $

$ab+\frac{1}{2}c^{2}$

；(用与 $ a $, $ b $, $ c $ 有关的代数式表示)
(2) 由(1)的结论证明勾股定理： $ a^2 + b^2 = c^2 $；
(3) 若 $ a + b = 7 $, $ c = 5 $,求 $ S_{\triangle ADC} $ 的值。

答案：
(1)$\frac{1}{2}ab$ $\frac{1}{2}ab$ $\frac{1}{2}c^{2}$ 或 $\frac{1}{2}(a^{2}+b^{2})$ $ab+\frac{1}{2}c^{2}$ 或 $\frac{1}{2}(a^{2}+b^{2})+ab$
(2)证明:$\because S_{四边形DB{C}'C}=ab+\frac{1}{2}c^{2}$,
又$\because S_{四边形DB{C}'C}=\frac{1}{2}(a+b)(a+b)$,
$\therefore ab+\frac{1}{2}c^{2}=\frac{1}{2}(a+b)(a+b)$,
$\therefore a^{2}+b^{2}=c^{2}$.
(3)解:$\because a+b=7$,$\therefore (a+b)^{2}=49$,即$a^{2}+b^{2}+2ab=49$.
$\because c=5$,且$a^{2}+b^{2}=c^{2}$,$\therefore a^{2}+b^{2}=25$,
$\therefore 25+2ab=49$,
$\therefore ab=12$,
$\therefore S_{\triangle ABC}=\frac{1}{2}ab=6$.

9. 数学老师在一次“探究性学习”中,设计了如下数表：

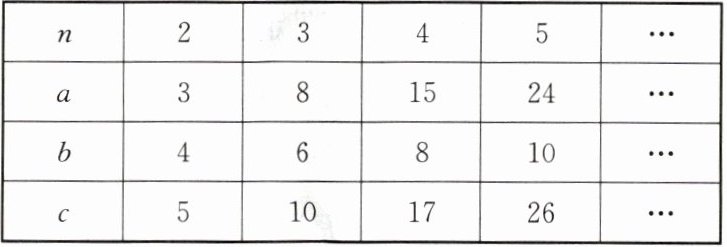
由表可知,当 $ n = 2 $ 时, $ a = 3 $, $ b = 4 $, $ c = 5 $。
(1) 当 $ n = 6 $ 时, $ a = $

, $ b = $

, $ c = $

；
(2) 请你观察 $ a $, $ b $, $ c $ 与 $ n (n ＞ 1) $ 之间的关系,分别用含 $ n $ 的代数式表示 $ a $, $ b $, $ c $,则 $ a = $

$n^{2}-1$

, $ b = $

$2n$

, $ c = $

$n^{2}+1$

；
(3) 猜想以 $ a $, $ b $, $ c $ 为三边的三角形是否为直角三角形,并说明理由。
解:以$a,b,c$为三边的三角形是直角三角形.理由:
$\because a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=(n^{2}+1)^{2}=c^{2}$,
$\therefore$以$a,b,c$为三边的三角形是直角三角形.

答案：
(1)35 12 37
(2)$n^{2}-1$ $2n$ $n^{2}+1$
(3)解:以$a,b,c$为三边的三角形是直角三角形.理由:
$\because a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=(n^{2}+1)^{2}=c^{2}$,
$\therefore$以$a,b,c$为三边的三角形是直角三角形.