2025年启东中学作业本八年级数学上册苏科版宿迁专版第33页解析答案

9. 如图,点 $ D $,$ E $,$ F $ 分别在等边三角形 $ ABC $ 的边 $ AB $,$ BC $,$ CA $ 上.若 $ AD = BE = CF $,试判断 $ \triangle DEF $ 的形状,并证明.

答案：解:△DEF为等边三角形.证明如下:$\because △ABC$为等边三角形,$\therefore AB=BC=CA,∠A=∠B=∠C=60^{\circ }.\because AD=BE=CF,\therefore BD=CE=AF,$$\therefore △ADF\cong △BED\cong △CFE,$$\therefore DF=ED=EF,\therefore △DEF$为等边三角形.

解析：

解：△DEF为等边三角形。证明如下：
∵△ABC为等边三角形，
∴AB=BC=CA，∠A=∠B=∠C=60°。
∵AD=BE=CF，
∴AB-AD=BC-BE=CA-CF，即BD=CE=AF。
在△ADF、△BED和△CFE中，
$\begin{cases}AD=BE=CF \\∠A=∠B=∠C \\AF=BD=CE\end{cases}$
∴△ADF≌△BED≌△CFE（SAS），
∴DF=ED=EF，
∴△DEF为等边三角形。

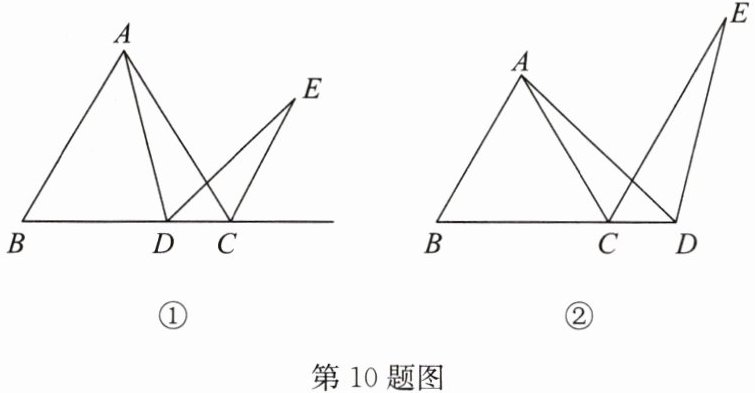
10. $ \triangle ABC $ 为等边三角形,$ D $ 为射线 $ BC $ 上一点,$ \angle ADE = 60^{\circ} $,$ DE $ 与 $ \triangle ABC $ 的外角平分线交于点 $ E $.
(1) 如图①,点 $ D $ 在 $ BC $ 边上,求证：$ CA = CD + CE $；
(2) 如图②,点 $ D $ 在 $ BC $ 的延长线上,请写出 $ CA $,$ CD $,$ CE $ 之间的数量关系,并说明理由.

答案：
$(1) $证明$:$如答图$①,$在$AC$上截取$CM = CD,$连接$DM.　$　　

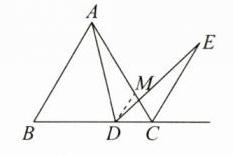
∵$△ABC$是等边三角形$,$
∴$∠ACB = 60°, $　　
∵$△CDM$是等边三角形$, $　　
∴$MD = CD = CM,∠CMD = ∠CDM = 60°, $　　
∴$∠AMD = 120°, $　　
∵$∠ADE = 60°,$
∴$∠ADE = ∠MDC, $　　
∴$∠ADM = ∠EDC. $　　
∵$DE$与$△ABC$的外角平分线交于点$E, $　　
∴$∠ACE = 60°,$
∴$∠DCE = 120° = ∠AMD. $　　
在$△ADM$和$△EDC$中$, $　　
$\begin{cases}\angle ADM=\angle EDC,\\ MD = CD,\\ \angle AMD=\angle ECD,\end{cases} $　　
∴$△ADM≌△EDC(ASA),$
∴$AM = EC, $　　
∴$CA = CM + AM = CD + CE. $　　
$(2) $解$:CA = CE - CD.$理由如下$: $　　
如答图$②,$在$AC$的延长线上截取$CM = CD,$连接$DM.$　　

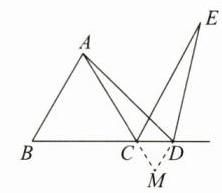
∵$△ABC$是等边三角形$,$
∴$∠ACB = 60°, $　　
∵$MD = CD,$
∴$∠CMD = ∠CDM = 60°, $　　
∵$DE$与$△ABC$的外角平分线交于点$E, $　　
∴$∠ACE = ∠DCE = 60°, $　　
∴$∠ECD = ∠AMD. $　　
∵$∠ADE = 60°,$
∴$∠ADE = ∠CDM, $　　
∴$∠ADM = ∠EDC. $　　
在$△ADM$和$△EDC$中$, $　　
$\begin{cases}\angle ADM=\angle EDC,\\ MD = CD,\\ \angle AMD=\angle ECD,\end{cases} $　　
∴$△ADM≌△EDC(ASA), $　　
∴$AM = EC,$
∴$CA = AM - CM = CE - CD. $　　

11. 如图,$ \triangle ABC $ 是等边三角形,$ D $ 是 $ \triangle ABC $ 外一点,且 $ \angle BDC = 120^{\circ} $,试探究线段 $ AD $,$ BD $,$ CD $ 之间的数量关系,并说明理由.

答案：
解:AD=BD + CD,理由如下:延长BD至点E,使DE=DC,连接CE,如图$.\because ∠BDC=120^{\circ },\therefore ∠CDE=60^{\circ },\therefore △CDE$是等边三角形$,\therefore CD=CE,∠DCE=60^{\circ }.\because △ABC$是等边三角形$,\therefore AC=BC,∠ACB=60^{\circ },\therefore ∠ACB+∠BCD=∠DCE+∠BCD,$即$∠ACD=∠BCE.\therefore △ACD\cong △BCE(SAS),\therefore AD=BE.\because BE=BD+DE,\therefore AD=BD+CD.$