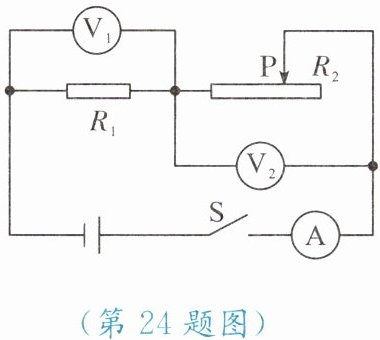
24. 如图所示的电路中,电源电压保持不变,滑动变阻器 $ R_2 $ 上标有“$ 80 \Omega \; 1 \mathrm{A} $”字样。闭合开关 $ \mathrm{S} $ 后,电流表 $ \mathrm{A} $ 的示数为 $ 0.5 \mathrm{A} $,电压表 $ \mathrm{V}_1 $ 的示数为 $ 10 \mathrm{V} $,电压表 $ \mathrm{V}_2 $ 的示数为 $ 6 \mathrm{V} $。求:
(1)定值电阻 $ R_1 $ 的阻值;
(2)当滑动变阻器 $ R_2 $ 接入电路的电阻为 $ 20 \Omega $ 时电流表的示数;
(3)当滑片移至最右端时,电压表 $ \mathrm{V}_2 $ 的示数。
答案:解:$(1)R_{1 }=\frac {U_{ 1 }}{I_{ }}=\frac {{ 10 }\ \text {V}}{{ 0.5 }\ \text {A}}={ 20 }Ω$
$ (2)U=10\ \text {V}+6\ \text {V}=16\ \text {V}$
$ I_{ }=\frac {U_{ }}{R_{1 }+R_2}=\frac {{ 16 }\ \text {V}}{{ 20 }Ω+20}={ 0.4 }\ \text {A}$
$ (3)U_2=\frac {R_2}{R_1+R_2}U=\frac {80\ \mathrm {Ω}}{20\ \mathrm {Ω}+80\ \mathrm {Ω}}×16\ \mathrm {V}=12.8\ \mathrm {V}$
25. 如图所示,电源电压保持不变,定值电阻 $ R_1 $ 规格为“$ * \Omega \; 0.5 \mathrm{A} $”,电流表量程为 $ 0 \sim 0.6 \mathrm{A} $,电压表量程为 $ 0 \sim 3 \mathrm{V} $,定值电阻 $ R_2 $ 的阻值为 $ 12 \Omega $,滑动变阻器 $ R_3 $ 的规格为“$ 12 \Omega \; 1 \mathrm{A} $”。当闭合开关 $ \mathrm{S} $ 和 $ \mathrm{S}_2 $、断开 $ \mathrm{S}_1 $ 时,电流表的示数为 $ 0.3 \mathrm{A} $,电压表的示数为 $ 2.4 \mathrm{V} $;当闭合开关 $ \mathrm{S} $ 和 $ \mathrm{S}_1 $、断开 $ \mathrm{S}_2 $ 时,调节滑动变阻器 $ R_3 $ 使其接入电路的电阻为 $ 7 \Omega $ 时,电压表的示数为 $ 2.8 \mathrm{V} $。求:
(1)电源电压。
(2)定值电阻 $ R_1 $ 的阻值。
(3)当闭合开关 $ \mathrm{S} $ 和 $ \mathrm{S}_1 $、断开 $ \mathrm{S}_2 $ 时,在保障电路安全的前提下,计算出滑动变阻器接入电路的取值范围。

答案:(1)6 V (2)8Ω (3)4~8Ω
解析:
(1)当闭合开关$S$和$S_2$、断开$S_1$时,$R_2$与$R_3$串联,电压表测$R_3$两端电压$U_3=2.4\mathrm{V}$,电流$I=0.3\mathrm{A}$。$R_2$两端电压$U_2=IR_2=0.3\mathrm{A}×12\Omega=3.6\mathrm{V}$,电源电压$U=U_2+U_3=3.6\mathrm{V}+2.4\mathrm{V}=6\mathrm{V}$。
(2)当闭合开关$S$和$S_1$、断开$S_2$时,$R_1$与$R_3$串联,$R_3=7\Omega$,电压表测$R_3$两端电压$U_3'=2.8\mathrm{V}$,电路电流$I'=\frac{U_3'}{R_3}=\frac{2.8\mathrm{V}}{7\Omega}=0.4\mathrm{A}$,$R_1$两端电压$U_1=U-U_3'=6\mathrm{V}-2.8\mathrm{V}=3.2\mathrm{V}$,$R_1=\frac{U_1}{I'}=\frac{3.2\mathrm{V}}{0.4\mathrm{A}}=8\Omega$。
(3)$R_1$允许最大电流$0.5\mathrm{A}$,电流表量程$0.6\mathrm{A}$,电路最大电流$I_{max}=0.5\mathrm{A}$,总电阻$R_{总min}=\frac{U}{I_{max}}=\frac{6\mathrm{V}}{0.5\mathrm{A}}=12\Omega$,$R_3$最小阻值$R_{3min}=R_{总min}-R_1=12\Omega-8\Omega=4\Omega$。电压表量程$3\mathrm{V}$,$R_3$两端最大电压$U_{3max}=3\mathrm{V}$,$R_1$两端电压$U_{1min}=U-U_{3max}=3\mathrm{V}$,最小电流$I_{min}=\frac{U_{1min}}{R_1}=\frac{3\mathrm{V}}{8\Omega}=0.375\mathrm{A}$,$R_3$最大阻值$R_{3max}=\frac{U_{3max}}{I_{min}}=\frac{3\mathrm{V}}{0.375\mathrm{A}}=8\Omega$,故$R_3$取值范围$4\Omega\sim8\Omega$。
(1)$6\mathrm{V}$
(2)$8\Omega$
(3)$4\Omega\sim8\Omega$