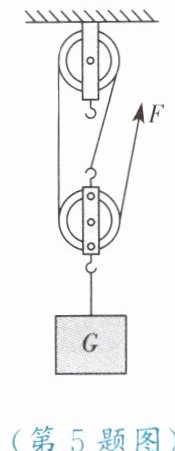
5. 如图所示为一个定滑轮和一个动滑轮组成的滑轮组,用它提升重为$900N$的物体,不考虑绳重和摩擦。问:
(1)若不计滑轮重,则所用的拉力$F$为多大?
(2)若实际所用的拉力$F为350N$,则动滑轮重多少牛?
(3)若要使物体上升$3m$,则需将绳子拉动多少米?
答案:解:$(1)F=\frac 13G=\frac 13×900\ \text {N}=300\ \text {N}$
$ (2)G_{动}=3F-G=3×350\ \text {N}-900\ \text {N}=150\ \text {N}$
$ (3)s=3h=3×3\ \text {m}=9\ \text {m}$
6. 如图所示,汽车通过滑轮组从竖直矿井中匀速提升矿石,矿石在$8s内上升8m$。已知矿石重$2700N$,动滑轮重$300N$,不计绳重及摩擦,在该过程中:
(1)该滑轮组既可以
省力
,又可以
改变施力的方向
。
(2)求汽车拉力的大小。
1000 N
(3)求汽车运动的速度。
3 m/s
(4)若绳子能承受的最大拉力为$1500N$,则汽车能提升矿石的最大重力是多少牛?
4200 N

答案:(1)省力 改变施力的方向 (2)1000 N (3)3 m/s (4)4200 N
解析:
(1)省力 改变施力的方向
(2)由图可知,连接动滑轮绳子的股数$n=3$,不计绳重及摩擦,汽车拉力$F=\frac{G+G_{动}}{n}=\frac{2700\,N+300\,N}{3}=1000\,N$
(3)矿石上升的速度$v_{物}=\frac{h}{t}=\frac{8\,m}{8\,s}=1\,m/s$,汽车运动的速度$v=nv_{物}=3×1\,m/s=3\,m/s$
(4)由$F=\frac{G+G_{动}}{n}$可得,汽车能提升矿石的最大重力$G_{max}=nF_{max}-G_{动}=3×1500\,N-300\,N=4200\,N$