2025年新课程自主学习与测评八年级数学上册人教版第63页解析答案

3. 如图,$ A $ 为马厩,$ B $ 为帐篷,牧马人某一天要从马厩牵出马,先到草地边 $ MN $ 某一处牧马,再到河边 $ l $ 某一处饮马,然后回到帐篷。请你在图中帮他确定这一天的最短路线。

答案：
如图,作点A关于MN的对称点A',作点B关于l的对称点B',连接A'B',分别交MN于点C,交l于点D,则A−C−D−B为确定的最短路线.

4. 如图,钝角三角形 $ ABC $ 的面积为 $ 15 $,最长边 $ AB = 10 $,$ BD $ 平分 $ \angle ABC $,点 $ M $,$ N $ 分别是 $ BD $,$ BC $ 上的动点,求 $ CM + MN $ 的最小值。

答案：CM+MN的最小值为3

解析：

证明：过点$C$作$CE \perp AB$于点$E$，交$BD$于点$M$，过点$M$作$MN \perp BC$于点$N$。
$\because BD$平分$\angle ABC$，$ME \perp AB$，$MN \perp BC$，
$\therefore ME = MN$。
$\because S_{\triangle ABC} = \frac{1}{2} × AB × CE = 15$，$AB = 10$，
$\therefore \frac{1}{2} × 10 × CE = 15$，解得$CE = 3$。
$\because CM + MN = CM + ME = CE$，
$\therefore CM + MN$的最小值为$3$。
$3$

5. 如图,四边形 $ ABCD $ 中,$ \angle C = 50^{\circ} $,$ \angle B = \angle D = 90^{\circ} $,$ E $,$ F $ 分别是 $ BC $,$ DC $ 上的点,当 $ \triangle AEF $ 的周长最小时,求 $ \angle EAF $ 的度数。

答案：∠EAF=80°

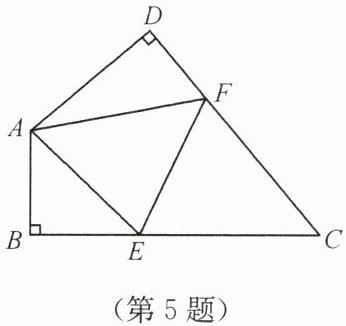
解析：

证明：作点$A$关于$BC$的对称点$A'$，关于$CD$的对称点$A''$，连接$A'A''$，分别交$BC$、$CD$于点$E$、$F$，此时$\triangle AEF$的周长最小。
由对称性得：$AE = A'E$，$AF = A''F$，$\angle A' = \angle BAE$，$\angle A'' = \angle DAF$。
在四边形$ABCD$中，$\angle BAD = 360^{\circ}-\angle B-\angle D-\angle C = 360^{\circ}-90^{\circ}-90^{\circ}-50^{\circ}=130^{\circ}$，故$\angle BAE+\angle DAF = 130^{\circ}-\angle EAF$。
在$\triangle A'A''A$中，$\angle A'+\angle A''=180^{\circ}-\angle BAD = 50^{\circ}$，即$\angle BAE+\angle DAF = 50^{\circ}$。
所以$130^{\circ}-\angle EAF = 50^{\circ}$，解得$\angle EAF = 80^{\circ}$。
$\angle EAF=80^{\circ}$