21. (12 分)【探索归纳】
(1)如图(1),已知 $\triangle ABC$ 为直角三角形,$\angle A = 90^{\circ}$,若沿图中虚线剪去 $\angle A$,则 $\angle 1 + \angle 2 = $。
(2)如图(2),已知在 $\triangle ABC$ 中,$\angle A = 40^{\circ}$,剪去 $\angle A$ 后成四边形,则 $\angle 1 + \angle 2 = $。
(3)如图(2),根据(1)与(2)的求解过程,请你归纳猜想 $\angle 1 + \angle 2$ 与 $\angle A$ 的关系是。
(4)如图(3),若没有剪掉 $\angle A$,而是把它折成如图所示形状,试探究 $\angle 1 + \angle 2$ 与 $\angle A$ 的关系并说明理由。

22. (12 分)【问题引入】
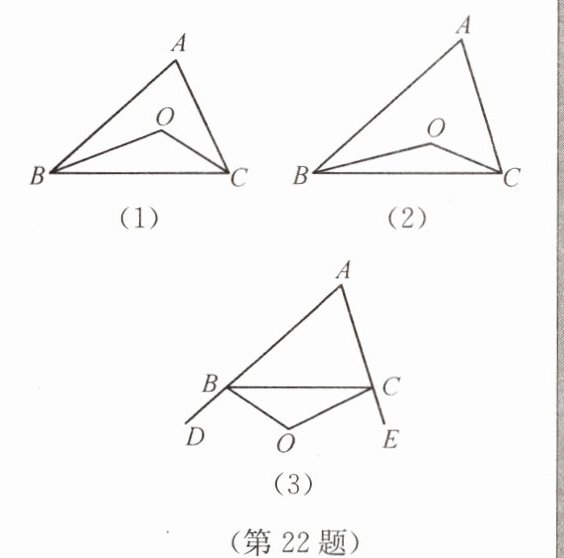
(1)如图(1),在 $\triangle ABC$ 中,点 $O$ 是 $\angle ABC$ 和 $\angle ACB$ 平分线的交点,若 $\angle A = \alpha$,则 $\angle BOC = $(用 $\alpha$ 表示)。
(2)如图(2),$\angle CBO = \frac{1}{3}\angle ABC$,$\angle BCO = \frac{1}{3}\angle ACB$,若 $\angle A = \alpha$,则 $\angle BOC = $(用 $\alpha$ 表示),并说明理由。
(3)如图(3),$\angle CBO = \frac{1}{3}\angle DBC$,$\angle BCO = \frac{1}{3}\angle ECB$,若 $\angle A = \alpha$,请猜想 $\angle BOC = $(用 $\alpha$ 表示),并说明理由。
【类比研究】
(4)若 $BO$,$CO$ 分别是 $\triangle ABC$ 的外角 $\angle DBC$,$\angle ECB$ 的 $n$ 等分线,它们交于点 $O$,$\angle CBO = \frac{1}{n}\angle DBC$,$\angle BCO = \frac{1}{n}\angle ECB$。若 $\angle A = \alpha$,请猜想 $\angle BOC = $(用 $\alpha$,$n$ 表示,直接写出结果)。