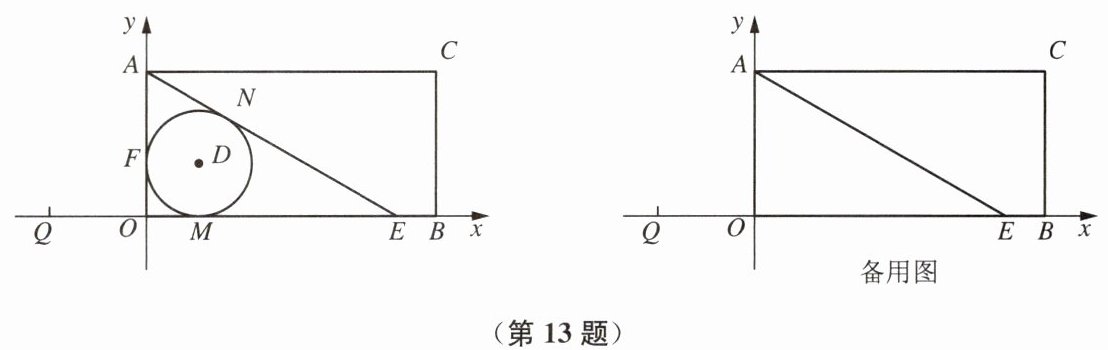
13. 如图,在矩形$AOBC$中,点$A$、$B的坐标分别为(0,6)$、$(12,0)$,点$E在边OB$上,$\angle AEO= 30^{\circ}$,点$P从点Q(-4,0)$出发,沿$x$轴以每秒1个单位长度的速度向右运动,运动时间为$t\ s$.
(1)求点$E$的坐标;
(2)若$\odot D与\triangle AOE$的三边相切,切点分别为$N$、$M$、$F$,求$\odot D$的半径;
(3)以点$P$为圆心,$PA为半径的\odot P随点P$的运动而变化,当$\odot P与四边形AEBC$的边(或边所在的直线)相切时,求$t$的值.
答案: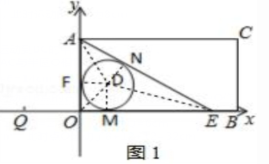
解:$( 1 )$
∵$A( 0,$$6 ) ,$$B( 12,$$0 ) ,$
∴$OA=6,$$OB=12,$
∵$∠AEO=30°,$
∴$AE=12,$
∴$OE=6\sqrt{3},$
∴点$E$的坐标$( 6\sqrt{3},$$0 )$
$(2)$如图$1,$连接$DA、$$DO、$$DB,$连接$DM、$$DN、$$DF,$
∵$\odot D$与三角形$AOE$的三边相切,切点分别为$N、$$M、$$F$
,
∴$DM⊥OB、$$DN⊥AB、$$DF⊥OA,$
则$S_{△AOE}=S_{△DAO}+S_{△DOE}+S_{△DAB}$
∴$\frac {1}{2}OE\cdot OA=\frac {1}{2}OA·DF+\frac {1}{2}OE·DM+\frac {1}{2}AE·DN$
∵$OA=6、$$OE=6\sqrt{3}、$$AE=12、$$DM=DN=DF=r,$
∴$\frac {1}{2}×6\sqrt{3}×6=\frac {1}{2}×6×r+\frac {1}{2}×6\sqrt{3}×r+\frac {1}{2}×12×r$
解得:$r=\frac {6\sqrt{3}×6}{6+6\sqrt{3}+12}=3\sqrt{3}-3$
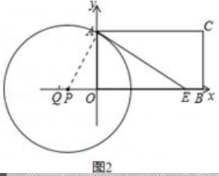
$( 3 ) ①$如图$2,$当$\odot P$与$AE$相切时,
∵$PA$是$\odot P$的半径,
∴点$A$为切点,
∵$OA=6,$$∠AEO=30°,$
∴$∠PAO=30°,$$OP=2\sqrt{3},$
∴$QP=4-2\sqrt{3},$
∴$t=( 4-2\sqrt{3} ) $秒$.$
$②$如图$3,$当点$P$与$O$重合时,$\odot P$与$AC$相切,
∴$t=4$秒$.$
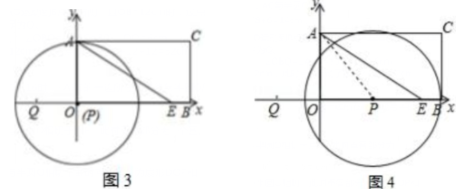
$③$如图$4,$当$PA=PB$时,$\odot P$与$BC$相切,设$OP=x,$
则$PB=PA=12-x,$
在$Rt△OAP $中,$x^2+6^2=( 12-x ) ^2,$解得:$x=\frac {9}{2},$
∴$t=4+\frac {9}{2}=\frac {17}{2}($秒$),$
∴$t=4-2\sqrt{3}$或$4$或$\frac {17}{2}$秒$.$