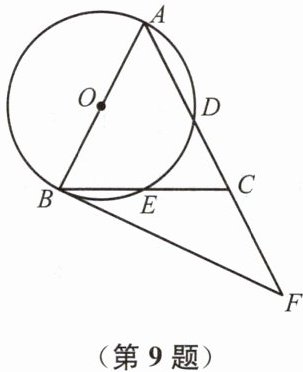
9. 如图,在$\triangle ABC$中,$AB= AC$,$\angle BAC= 54^{\circ}$,以$AB为直径的\odot O分别交AC$、$BC于点D$、$E$,过点$B作\odot O$的切线,交$AC的延长线于点F$.
(1)求证:$BE= CE$;
(2)求$\angle CBF$的度数;
(3)若$AB= 6$,求$\overset{\frown}{AD}$的长.
答案:证明:(1) 连接AE,
∵AB=AC∴△ABC为等腰三角形
∵AB为$\odot O$的直径
∴AE⊥BC∴BE=CE
(2) ∵△ABC为等腰三角形且AE⊥BC
∴AE平分∠BAC∴∠BAC=54°
∴$∠BAE=\frac {1}{2}∠BAC=27°$
∵∠AEB=90°
∴∠ABE=180°-90°-27°=63°
∵BF为$\odot O$的切线
∴∠OBF=90°
∴∠CBF=∠OBF-∠ABE=90°-63°=27°
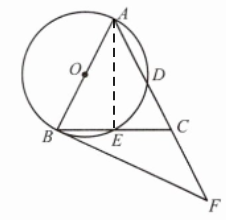
解:(3) 连接OD,
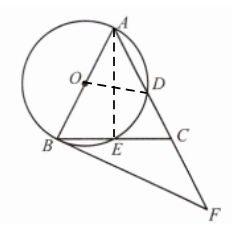
∵∠BAC=54°,OA=OD
∴∠ODA=∠BAC=54°
∴∠AOD=180°-54°-54°=72°
∵AB=6
∴$\odot O$的半径为3
∴$\overset{\LARGE{ \frown}}{AD}=\frac {72\pi ×3}{180}=\frac {6}{5}\pi$