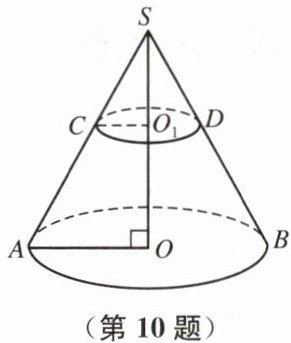
10. 如图,有一个圆锥,其高 $SO= 20\sqrt{2}\ cm$,母线 $SA= 30\ cm$.
(1)求此圆锥侧面展开图的圆心角;
(2)若在此圆锥的上面截去一个高为 $10\sqrt{2}\ cm$ 的圆锥,求剩下的几何体侧面展开图的面积.
答案:(1)$120^\circ$;(2)$225\pi$
解析:
(1)在Rt△SOA中,SO=20√2 cm,SA=30 cm,
OA=√(SA²-SO²)=√(30²-(20√2)²)=√(900-800)=√100=10 cm,
圆锥底面周长=2π·OA=2π×10=20π cm,
设侧面展开图圆心角为n°,则(nπ·SA)/180=20π,
(nπ×30)/180=20π,n=120,
故圆心角为120°。
(2)截去圆锥的高SO₁=10√2 cm,原圆锥高SO=20√2 cm,
则SO₁/SO=1/2,由相似知O₁C/OA=SO₁/SO=1/2,O₁C=5 cm,
截去圆锥底面周长=2π·O₁C=10π cm,
原圆锥侧面积=(1/2)×20π×30=300π cm²,
截去圆锥侧面积=(1/2)×10π×(SA/2)=(1/2)×10π×15=75π cm²,
剩下几何体侧面展开图面积=300π-75π=225π cm²。
11. 工人师傅要把一块矩形铁皮加工成一个底面半径为 20 cm、高为 $40\sqrt{2}\ cm$的圆锥形漏斗,要求只有一条接缝(接缝尺寸忽略不计).请你设计两种不同的裁剪方案画图并计算,比较哪种方案用料最少.此时所需矩形铁皮的长、宽分别为多少?
答案:解:圆锥的母线长:
${\sqrt {{20}^{2}+{(40{\sqrt {2}})}^{2}}}=60(cm)$
设这个圆锥展开后的圆心角为n°
,则${\frac {nπ×60} {180}}=2π×20$
解得,n=120
方案一如图1,
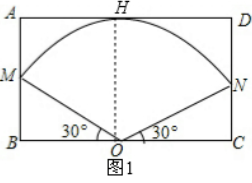
OM=OH=60cm,∠MON=120°
在Rt△OBM中,
∵ OM=60cm,∠MOB=30°
∴BM=30cm,
$OB={\sqrt {{OM}^{2}-{BM}^{2}}}=30{\sqrt {3}}cm$
∴$ BC=2OB=60\sqrt {3}cm$
∴ 方案一所需矩形铁皮的面积:
$60×60{\sqrt {3}}=3600{\sqrt {3}}(cm^2)$
方案二如图2,
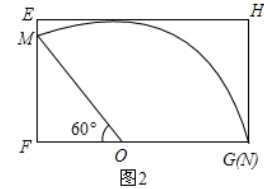
OM=EF=60cm,∠MON=120°
在Rt△MOF中,
∵ OM=60cm,∠MOF=60°
∴$ OF=\frac 1 2OM=30cm$
∴ FG=OF+OG=90cm
∴ 方案二所需矩形铁皮的面积:
$90×60=5400(cm^2)$
∵$ 5400<3600\sqrt {3}$
∴ 方案二用料最少,此时所需矩形铁
皮的长为90cm,宽为60cm.