9. 如图,P(x,y)为函数 y= 3/2x 的图像上的一个动点,⊙P 的半径为 3,
(1) 求⊙P 与过点(2,0)且与 y 轴平行的直线相切时点 P 的坐标;
(2) 请分别写出⊙P 与过点(2,0)且与 y 轴平行的直线相交、相离时 x 的取值范围.
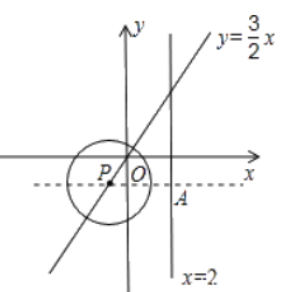
答案:解:(1)过P作直线x=2的垂线,垂足为A.
当点P在直线x=2右侧时,
AP=x-2=3,得x=5.∴P(5,$\frac {15}{2}).$
当点P在直线x=2左侧时,
PA=2-x=3,得x=-1.∴P(-1,$-\frac {3}{2}).$
∴当⊙P与直线x=2相切时,点
P的坐标为(5,$\frac {15}{2})$或(-1,$-\frac {3}{2}).$
(2)当-1<x<5时,⊙P与直线x=2相交.
当x<-1或x>5时,⊙P与直线x=2相离.
解析:
(1)过点$(2,0)$且与$y$轴平行的直线为$x=2$。
点$P(x,y)$到直线$x=2$的距离为$|x - 2|$。
因为$\odot P$与直线$x=2$相切,且半径为$3$,所以$|x - 2| = 3$。
当$x - 2 = 3$时,$x = 5$,则$y=\frac{3}{2}×5=\frac{15}{2}$,点$P$坐标为$(5,\frac{15}{2})$;
当$x - 2 = -3$时,$x = -1$,则$y=\frac{3}{2}×(-1)=-\frac{3}{2}$,点$P$坐标为$(-1,-\frac{3}{2})$。
所以点$P$的坐标为$(-1,-\frac{3}{2})$或$(5,\frac{15}{2})$。
(2)当$\odot P$与直线$x=2$相交时,$|x - 2| < 3$,解得$-1 < x < 5$;
当$\odot P$与直线$x=2$相离时,$|x - 2| > 3$,解得$x < -1$或$x > 5$。
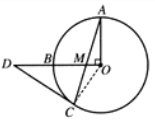
例1 如图2.5.2,OA、OB是⊙O中互相垂直的两条半径,M是OB上任一点,连接AM并延长交⊙O于点C,过点C作直线交MB的延长线于点D,如果满足条件DM= DC,那么直线CD是⊙O的切线吗? 请说明理由.

答案:解:CD是⊙O的切线,理由如下:
连接OC,
∵ DM=DC∴ ∠DCM=∠DMC=∠AMO
∵ AO⊥DO∴ ∠AOM=90°
∴ ∠AMO+∠MAO=90°
∵ OA=OC∴ ∠MAO=∠MCO
∴ DCM+∠MCO=90°,
即∠DCO=90°
∴ CD是⊙O的切线
解析:
直线CD是⊙O的切线,理由如下:
连接OC。
∵OA=OC,
∴∠OAC=∠OCA。
∵OA⊥OB,
∴∠OAC+∠OMA=90°。
∵DM=DC,
∴∠DMC=∠DCM。
∵∠OMA=∠DMC,
∴∠OCA+∠DCM=∠OAC+∠OMA=90°,即∠OCD=90°。
∵OC是⊙O的半径,
∴直线CD是⊙O的切线。