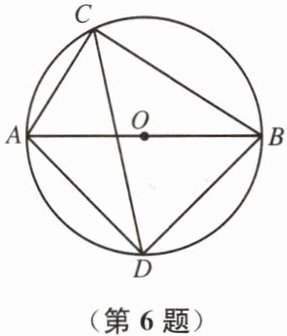
6. 如图,$\odot O$的直径 AB 为 10 cm,弦 AC 为 6 cm,$∠ACB的平分线交\odot O$于点 D.求 BC、AD、BD 的长.
答案:解:∵ AB为⊙O的直径∴ ∠ACB=∠ADB=90°
在Rt△ABC中,∵ AC=6cm,AB=10cm
∴$ BC={\sqrt {{AB}^{2}-{AC}^{2}}}=8cm$
∵ CD平分∠ACB∴ ∠ACD=∠BCD
∴$ {\widehat{AD}}={\widehat{BD}}$∴ AD=BD
在Rt△ABD中,∵ AD=BD
∴$ AB={\sqrt {{AD}^{2}+{BD}^{2}}}={\sqrt {2}}AD$
∵ AB=10cm
∴$ AD=BD=5\sqrt {2}cm$
解析:
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°。
在Rt△ABC中,AB=10cm,AC=6cm,
由勾股定理得:BC=$\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=8$cm。
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴$\overset{\frown}{AD}=\overset{\frown}{BD}$,
∴AD=BD。
在Rt△ADB中,AD=BD,AB=10cm,
设AD=BD=x,由勾股定理得:$AD^{2}+BD^{2}=AB^{2}$,
即$x^{2}+x^{2}=10^{2}$,
解得$x=5\sqrt{2}$,
∴AD=BD=$5\sqrt{2}$cm。
综上,BC=8cm,AD=BD=$5\sqrt{2}$cm。
7. 如图,AB 为$\odot O$的直径,点 C 在$\odot O$上,延长 BC 到点 D,使$DC= CB$,延长 DA 交$\odot O$于点 E,连接 AC、CE.
(1) 求证:$CD= CE;$
(2) 若$AB= 4,BC-AC= 2$,求 CE 的长.

答案:证明:(1) ∵AB为$\odot O$直径
∴∠ACB=∠ACD=90°
在△ADC和△ABC中,
∴△ADC≌△ABC( SAS )
∴∠D=∠B.∵∠B=∠E∴∠D=∠E
∴CD=CE
( 2 ) 解:设BC=x,则AC=x-2
在Rt△ABC中,由勾股定理可知,
$AB^2=AC^2+BC^2$
∵AB=4,BC=x,AC=x-2
∴$4^2=( x-2 ) ^2+x^2$
解得,$x_1=1+\sqrt{7}\text{,}$
$x_2=1-\sqrt{7}( $不合题意,舍去 )
∴$BC=1+\sqrt{7}$
∵BC=CD=CE
∴$CE=1+\sqrt{7}. $
8. 如图,在平面直角坐标系中,$\odot C$过原点,并与坐标轴分别交于点 A、D,$∠OBA= 30^{\circ }$,点 D 的坐标为$(0,3)$,则点 A、C 的坐标分别为
$(-\sqrt{3},0)$
,
$(-\frac {\sqrt{3}}{2},\frac {3}{2})$
.
答案:$(-\sqrt{3},$0)
$(-\frac {\sqrt{3}}{2},$$\frac {3}{2})$
解析:
连接AD,
∵∠AOD=90°,
∴AD为⊙C的直径,
∵点D的坐标为(0,3),
∴OD=3,
∵∠OBA=30°,∠OBA=∠ODA,
∴∠ODA=30°,
在Rt△AOD中,tan∠ODA=$\frac{OA}{OD}$,
即tan30°=$\frac{OA}{3}$,
$\frac{\sqrt{3}}{3}$=$\frac{OA}{3}$,
OA=$\sqrt{3}$,
∵点A在x轴负半轴,
∴点A的坐标为(-$\sqrt{3}$,0),
∵AD为直径,点A(-$\sqrt{3}$,0),点D(0,3),
∴点C为AD中点,
C点横坐标为$\frac{-\sqrt{3}+0}{2}$=-$\frac{\sqrt{3}}{2}$,
C点纵坐标为$\frac{0+3}{2}$=$\frac{3}{2}$,
∴点C的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$)
$(-\sqrt{3},0)$,$\left(-\dfrac{\sqrt{3}}{2},\dfrac{3}{2}\right)$
9. 如图,在$Rt\triangle ABC$中,$AB⊥BC,AB= 6,BC= 4$,P 是$\triangle ABC$内的一个动点,且满足$∠PAB= ∠PBC$,则线段 CP 长的最小值为(
B
)
A.$\frac {3}{2}$
B.2
C.$\frac {8\sqrt {13}}{13}$
D.$\frac {12\sqrt {13}}{13}$
答案:B
解析:
∵AB⊥BC,
∴∠ABC=90°,即∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°.
∴点P在以AB为直径的圆上.设AB中点为O,AB=6,则OA=OB=3,⊙O半径r=3.
连接OC,在Rt△OBC中,OB=3,BC=4,
∴OC=$\sqrt{OB^2+BC^2}=\sqrt{3^2+4^2}=5$.
∵点P在⊙O上,
∴CP≥OC-r=5-3=2.
∴线段CP长的最小值为2.
B