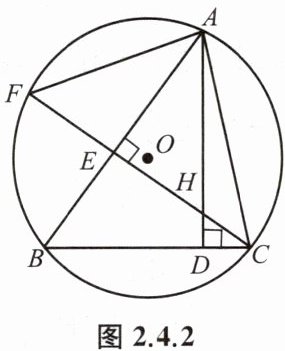
例2 如图2.4.2,A、B、C三点在⊙O上,△ABC的高AD、CE相交于点H,CE的延长线交⊙O于点F.
求证:AF= AH.
答案:证明:∵AD、CE为△ABC的高
∴∠BDH=∠BEH=90°
∵四边形BEHD的内角和为360°
∴∠B+∠EHD=180°
∵∠EHD+∠EHA=180°
∴∠B=∠EHA
∵∠B=∠F
∴∠F=∠EHA
∴AF=AH
1. 如图,A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿O—C—D—O的路线做匀速运动.设运动时间为t s,∠APB的度数为y°,下列图像中,最能恰当表示y与t之间函数关系的是(
C
)
答案:C
2. 如图,点D在⊙O的弦BC的延长线上,∠ACD= 110°,则∠AOB=
140
°.
答案:140
解析:
∵∠ACD=110°,
∴∠ACB=180°-∠ACD=70°,
∴∠AOB=2∠ACB=140°。
140
3. 如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=
90°
.
答案:90°
解析:
连接AD、BC。因为AB是⊙O的直径,所以∠ACB=90°,∠ADB=90°。∠1是圆周角,所对弧为AE;∠2是圆周角,所对弧为BE。∠1+∠2所对弧为AE+BE=AB。因为AB是直径,所对圆心角为180°,所以∠1+∠2=1/2×180°=90°。
$90^\circ$