答案：$\frac{3}{4}$

答案：1. **（1）
三个景点的游玩顺序总共有$A_{3}^3=\frac{3!}{(3 - 3)!}=3×2×1 = 6$种（排列数公式$A_{n}^m=\frac{n!}{(n - m)!}$）。
“南长街”作为游玩的第一个景点时，剩下两个景点的排列顺序有$A_{2}^2=\frac{2!}{(2 - 2)!}=2×1=2$种。
根据古典概型概率公式$P(A)=\frac{m}{n}$（其中$n$是基本事件总数，$m$是事件$A$包含的基本事件数），所以“南长街”作为游玩的第一个景点的概率$P=\frac{2}{6}=\frac{1}{3}$。
2. **（2）
解：由（1）知，三个景点游玩顺序的总情况数$n = A_{3}^3=6$种。
游玩顺序为“南长街”、“鼋头渚”、“惠山古镇”这$1$种情况，即$m = 1$。
根据古典概型概率公式$P=\frac{m}{n}$，这里$n = 6$，$m = 1$，所以游玩顺序为“南长街”、“鼋头渚”、“惠山古镇”的概率$P=\frac{1}{6}$。
综上，（1）答案为$\frac{1}{3}$；（2）游玩顺序为“南长街”、“鼋头渚”、“惠山古镇”的概率为$\frac{1}{6}$。

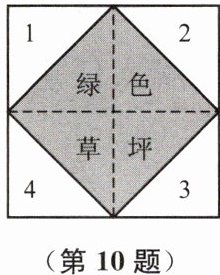
答案：解：(1)将大正方形分成8个全等的等腰直角三角形，
其中草坪占4个。
∵每次跳伞落在8个等腰直角三角形的可能性是相等的
∴一共有8种等可能的结果，其中一次跳伞落在草坪上有4种结果
∴P(一次跳伞落在草坪上$)=\frac 48=\frac 12$
(2)一共有8×8=64种等可能的结果，其中两次落在草坪上有4×4=16种结果
∴P(两次跳伞都落在草坪上$)=\frac {16}{64}=\frac 14$