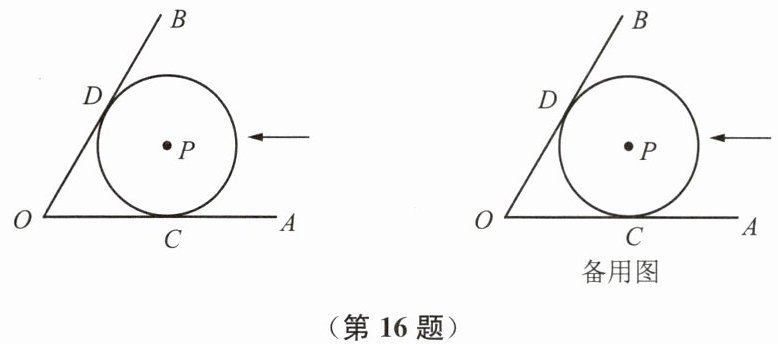
16. (本题12分)已知∠AOB= 60°,半径为3 cm的⊙P沿边OA从右向左移动,与边OA相切的切点记为C.
(1) 当⊙P移动到与边OB相切时(如图),记切点为D,求劣弧CD的长;
(2) 当⊙P移动到与边OB相交时,记交点为E、F,若EF= 4√2 cm,求OC的长.
答案:解:$\left( 1 \right) $连接$PD,$$PC.\ $
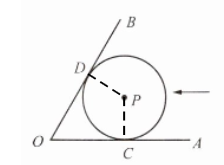
∵$OA、$$OB$都为$\odot P$的切线$\ $
∴$∠ODP=∠OCP=90°\ $
∵$∠AOB=60°\ $
∴$∠DPC=360°-90°-90°-60°=120° $
∵$\odot P$的半径为$3\,\,cm\ $
∴劣弧$CD$的长为
$\frac{120\pi ×3}{180}=2\pi \,\,cm\ $
解:$\left( 2 \right) $分两种情况$∶$
$①$点$P$在$∠AOB$内,连接$PE,PC,CP$的延
长线$ $与直线$OF$交于点$N,$$ $
过点$P$作$PM⊥EF,$垂足为点$M,$
如图$1\ $
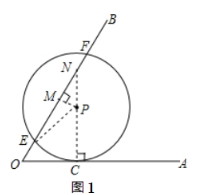
∵$EF=4\sqrt{2}\,\,cm,$$PM⊥EF\ $
∴$EM=\frac{1}{2}EF=2\sqrt{2}\,\,cm\ $
在$Rt△EPM$中,
∵$PE=3\,\,cm,$$EM=2\sqrt{2}\,\,cm\ $
∴$PM=\sqrt{PE^2-EM^2}=1\,\,cm\ $
∵$∠AOB=60°,∠OCP=90°\ $
∴$∠ONC=30°\ $
在$Rt△MNP$中$,$
∵$∠ONC=30°,$$PM=1\,\,cm\ $
∴$PN=2PM=2\,\,cm\ $
∵$\odot O$的半径为$3\,\,cm\ $
∴$CN=CP+PN=3\,\,cm+2\,\,cm=5\,\,cm$
$\ $在$Rt△OCN$中,
∵$∠ONC=30°,\ CN=5\,\,cm\ $
∴$OC=\frac{CN}{\sqrt{3}}=\frac{5\sqrt{3}}{3}\,\,cm\ $
$②$点$P$在$∠AOB$外,
连接$PF,$$PC,$$PC$与$EF$交于点$N,\ $
过点$P$作$PM⊥EF,$垂足为点$M,$如图$2$

$\ $
由$①$可知,
$PM=1\,\,cm,$$∠PNM=30°,$
$PN=2\,\,cm\ $
∵$PC=3\,\,cm\ $
∴$CN=PC-PN=1\,\,cm\ $
在$Rt△OCN$中,
∵$∠ONC=30°,$$CN=1\,\,cm\ $
∴$OC=\frac{CN}{\sqrt{3}}=\frac{\sqrt{3}}{3}\,\,cm$
$\ $综上所述,$OC$的长为$\frac{5\sqrt{3}}{3}\,\,cm$或$\frac{\sqrt{3}}{3}\ cm. $