20. (本题10分)如图,已知正方形ABCD的边长为4 cm,动点P从点B出发,以2 cm/s的速度沿B→C→D方向向点D运动;动点Q从点A出发,以1 cm/s的速度沿A→B方向向点B运动. 若P、Q两点同时出发,运动时间为t s.
(1) 连接PD、PQ、DQ,当t为何值时,△PQD的面积为$11 cm^2?$
(2) 当点P在BC上运动时,是否存在这样的t,使得△PQD是以PD为一腰的等腰三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由.
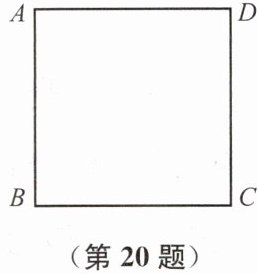
答案:解:(1)分两种情况:
①当0≤t≤ 2,点P在BC上时,如图
$14^2-\frac 12×4×t-\frac 12×(4-t)×2t-\frac 12×(4-2t)×4=11$
解得,$ t_1=3($舍去),$t_2= -1($舍去)
②当$2\lt t≤4,$点P在CD上时,如图2
$\frac 12×4× (8- 2t)= 11$解得,$t=\frac 54($舍去)
∴综上所述,不存在符合条件的t值,使△PQD的面积为$11\ \mathrm {cm}²$
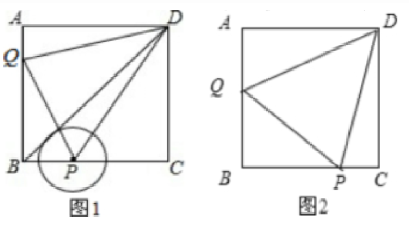
解:(2)存在
∵点P在BC上运动
∴0≤t≤2
∵△PQD是以PD为一腰的等腰三角形
∴PD=QD或PD=PQ
①PD=QD
$(4-2t)^2+4^2=t^2+4^2$
解得,$ t_1=\frac 43,$$t_2=4($舍去)
②PD=PQ
$(4 -2t)^2+4^2=(2t)^2+(4-t)^2$
解得,$ t_1=4\sqrt {2}-4,$
$t_2=-4\sqrt {2}-4($舍去)
∴综上所述,$ t=\frac 43$或$t=\sqrt {2}-4 $