活动一:做一做 填一填
1. 完成课本第 122~123 页的"活动"并填空:
(1)点P(1,-3)关于x轴的对称点P'的坐标为
(1, 3)
.
(2)点P(1,-3)关于y轴的对称点P''的坐标为
(-1, -3)
.
(3)点P'与点P''位置上有何关系?坐标之间有何联系?
点P'与点P''关于原点对称;坐标之间横坐标和纵坐标都互为相反数。
2. 归纳:如果点P的坐标为(a,b),那么点P关于x轴对称的点的坐标为
(a, -b)
,关于y轴对称的点的坐标为
(-a, b)
,关于坐标原点O对称的点的坐标为
(-a, -b)
.
答案:(1) $(1, 3)$
(2) $(-1, -3)$
(3) 点$P'$与点$P''$关于原点对称;坐标之间横坐标和纵坐标都互为相反数。
归纳:$(a, -b)$;$(-a, b)$;$(-a, -b)$
解析:
(1) 点$P(1, -3)$关于$x$轴对称,横坐标不变,纵坐标取反,所以对称点$P'$的坐标为$(1, 3)$。
(2) 点$P(1, -3)$关于$y$轴对称,纵坐标不变,横坐标取反,所以对称点$P''$的坐标为$(-1, -3)$。
(3) 点$P'$与点$P''$关于$z$轴(在这里是二维平面,因此可以理解为直线$y=x$或$y=-x$的对称性质,但在二维坐标系中直接观察可知它们关于原点对称)对称(在二维坐标系中表现为关于原点对称),坐标之间的联系是横坐标和纵坐标都互为相反数。
归纳:
如果点$P$的坐标为$(a, b)$,
那么点$P$关于$x$轴对称的点的坐标为$(a, -b)$,
关于$y$轴对称的点的坐标为$(-a, b)$,
关于坐标原点$O$对称的点的坐标为$(-a, -b)$。
活动二:试一试 想一想
如图4-3,在平面直角坐标系中描点,并填空:
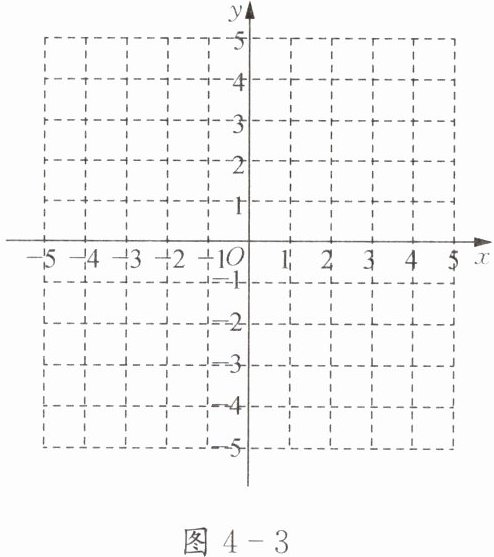
(1)将点P(2,0)绕原点按逆时针方向旋转90°后得到点P',点P'的坐标为
(0, 2)
;
(2)将点P(2,0)绕原点按逆时针方向旋转45°后得到点P'',点P''的坐标为
($\sqrt{2}$, $\sqrt{2}$)
.
答案:(1)$(0, 2)$,(2)$(\sqrt{2}, \sqrt{2})$。
解析:
(1) 点$P(2,0)$在$x$轴正半轴上,距离原点2个单位长度。当它绕原点逆时针旋转$90^\circ$后,会落在$y$轴正半轴上,距离原点仍然是2个单位长度,此时坐标变为$(0,2)$。
(2) 利用旋转矩阵或者构造等腰直角三角形来求解。
设$P''(x,y)$,由于旋转$45^\circ$,可以通过构造等腰直角三角形来求解。
过$P''$作$P''H\perp x$轴于点$H$。
在$Rt\triangle OPH$中,$OP=\sqrt{2^2}=2$。
$\because\angle POP''=45^\circ$。
$\therefore OH=PH=\sqrt{2}$。
$\because P''$在第二象限。
$\therefore P''$坐标为$(\sqrt{2},\sqrt{2})$。
活动三:议一议 说一说
(1)将点P(2,3)绕原点按逆时针方向旋转90°后得到点P',点P'的坐标为
(-3, 2)
;
(2)将点P(2,3)绕点(1,0)按逆时针方向旋转90°后得到点P'',点P''的坐标为
(-2, 1)
.
答案:(1) $(-3, 2)$
(2) $(-2, 1)$
解析:
(1) 点$P(2,3)$绕原点按逆时针方向旋转$90^\circ$,根据旋转的性质,点$P'$的坐标可以通过旋转矩阵计算得到,或者通过几何方法得到。在二维坐标系中,一个点$(x, y)$绕原点逆时针旋转$90^\circ$后的新坐标是$(-y, x)$。
因此,点$P(2,3)$旋转后的坐标是$(-3, 2)$。
(2) 对于点$P(2,3)$绕点$(1,0)$逆时针旋转$90^\circ$,可以先将点$P$平移到以$(1,0)$为原点的新坐标系中,然后应用旋转,最后再平移回原坐标系。
点$P$在新坐标系中的坐标是$(2-1, 3-0) = (1,3)$。
旋转后,新坐标系中的点$P''$的坐标是$(-3,1)$(应用$(-y, x)$的规则)。
再平移回原坐标系,得到$P''$的坐标是$(-3+1, 1+0) = (-2,1)$,或者通过向量运算$\vec{OP''} = \vec{OP} × R(\theta) + \vec{O'}$,其中$R(\theta)$是旋转矩阵,$\vec{O'}$是旋转中心的坐标。