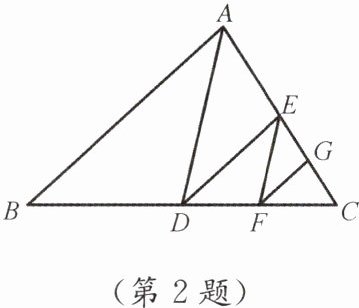
2. 如图,AD是△ABC的中线,DE是△ADC的中线,EF是△DEC的中线,FG是△EFC的中线.
(1)△ABD与△ADC的面积有何关系?请说明理由.
(2)若△GFC的面积为1,求△ABC的面积$S_{\triangle ABC}$.
答案:16
解析:
(1)根据中线的性质,三角形的中线将三角形分成面积相等的两部分。
因为$AD$是$\triangle ABC$的中线,所以$D$是$BC$的中点,即$BD = DC$。
所以$\triangle ABD$和$\triangle ADC$等底同高,即$S_{\triangle ABD} = S_{\triangle ADC} $,
即$\triangle ABD$与$\triangle ADC$的面积相等,都为$\triangle ABC$面积的一半。
(2)由于$AD$是$\triangle ABC$的中线,所以$S_{\triangle ABD} = S_{\triangle ADC} =\frac{1}{2}S_{\triangle ABC} $。
同理,$DE$是$\triangle ADC$的中线,所以$S_{\triangle ADE} = S_{\triangle CDE} =\frac{1}{2}S_{\triangle ADC}=\frac{1}{4}S_{\triangle ABC} $。
$EF$是$\triangle DEC$的中线,所以$S_{\triangle DFE} = S_{\triangle EFC} =\frac{1}{2}S_{\triangle DEC}=\frac{1}{8}S_{\triangle ABC} $。
$FG$是$\triangle EFC$的中线,所以$S_{\triangle EFG} = S_{\triangle GFC} =\frac{1}{2}S_{\triangle EFC}=\frac{1}{16}S_{\triangle ABC} $。
已知$S_{\triangle GFC} = 1$,所以$\frac{1}{16}S_{\triangle ABC}=1$,
因此,$S_{\triangle ABC} = 1 × 16 = 16$。
3. 如图,在△ABC中,CD,CE分别是△ABC的高和角平分线,∠BAC= α,∠B= β(α>β).
(1)若α= 70°,β= 40°,求∠DCE的度数;
(2)试用含α,β的代数式表示∠DCE的度数(直接写出结果).

答案:(1)$15^\circ$ (2)$\frac{1}{2}(\alpha - \beta)$
解析:
(1)因为$\alpha= 70^\circ$,$\beta= 40^\circ$,
所以$\angle ACB = 180^\circ - \angle BAC - \angle B = 180^\circ - 70^\circ - 40^\circ = 70^\circ$。
因为$CE$是$\angle ACB$的角平分线,
所以$\angle ACE = \frac{1}{2} \angle ACB = \frac{1}{2} × 70^\circ = 35^\circ$。
因为$CD$是$\triangle ABC$的高,
所以$\angle ADC = 90^\circ$,
所以$\angle ACD = 90^\circ - \angle BAC = 90^\circ - 70^\circ = 20^\circ$。
所以$\angle DCE = \angle ACE - \angle ACD = 35^\circ - 20^\circ = 15^\circ$。
(2)因为$\angle ACB = 180^\circ - \alpha - \beta$。
因为$CE$是$\angle ACB$的角平分线,
所以$\angle ACE = \frac{1}{2} \angle ACB = \frac{1}{2} (180^\circ - \alpha - \beta)$。
因为$CD$是$\triangle ABC$的高,
所以$\angle ADC = 90^\circ$,
所以$\angle ACD = 90^\circ - \alpha$。
所以$\angle DCE = \angle ACE - \angle ACD = \frac{1}{2} (180^\circ - \alpha - \beta)-(90^\circ - \alpha)=\frac{1}{2}(\alpha - \beta)$。