2. 如图,在△ABC中,AB= AC= 8,AD是底边上的高,E是AC的中点,则DE=
4
.
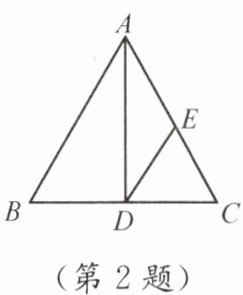
答案:4
解析:
在△ABC中,AB=AC,AD是底边上的高,所以AD⊥BC,∠ADC=90°(等腰三角形三线合一)。在Rt△ADC中,E是AC的中点,所以DE=1/2AC(直角三角形斜边中线等于斜边一半)。因为AC=8,所以DE=1/2×8=4。
3. 如图,等边三角形ABC的边长为3,点D在边BC上,且BD= 1,AD与BE相交于点P,若∠APE= 60°,则CE的长为______
1
$.zyjl.cn/pic18/2025-09-04/f2986f470420e6fabce1bd91a3bc4f82.jpg?x-oss-process=image/crop,x_1049,y_314,w_275,h_305">$
答案:1
解析:
∵△ABC为等边三角形,∴AB=AC=BC=3,∠BAC=∠ABC=∠ACB=60°.
∵∠APE=60°,∠BAC=60°,在△APE中,∠PAE+∠PEA=180°-∠APE=120°;在△ABE中,∠ABE+∠AEB=180°-∠BAC=120°.
∵∠PEA=∠AEB(公共角),∴∠PAE=∠ABE,即∠CAD=∠ABE.
在△ABE和△CAD中,∠ABE=∠CAD,AB=CA,∠BAE=∠ACD=60°,∴△ABE≌△CAD(ASA).
∴AE=CD.∵CD=BC-BD=3-1=2,∴AE=2,∴CE=AC-AE=3-2=1.
4. 如图,点D,E在△ABC的边BC上,AD= AE,BD= CE.试说明△ABC是等腰三角形.

答案:∵AD=AE,
∴∠ADE=∠AED(等边对等角)。
∵∠ADE+∠ADB=180°,∠AED+∠AEC=180°,
∴∠ADB=∠AEC(等角的补角相等)。
在△ABD和△ACE中,
∵AD=AE,∠ADB=∠AEC,BD=CE,
∴△ABD≌△ACE(SAS)。
∴AB=AC(全等三角形对应边相等)。
∴△ABC是等腰三角形。
5. 如图,BD= DC,DE⊥BC,交∠BAC的平分线于点E,EM⊥AB,EN⊥AC,垂足分别为M,N.求证:BM= CN.

答案:连接EB,EC。
∵AE平分∠BAC,EM⊥AB,EN⊥AC,
∴EM=EN(角平分线上的点到角两边距离相等)。
∵BD=DC,DE⊥BC,
∴DE垂直平分BC,
∴EB=EC(垂直平分线上的点到线段两端距离相等)。
在Rt△EMB和Rt△ENC中,
∵EB=EC,EM=EN,
∴Rt△EMB≌Rt△ENC(HL),
∴BM=CN。
1. 在Rt△ABC中,∠C= 90°,AD平分∠BAC,交BC于点D,若CD= 4,则点D到AB的距离是
4
.
答案:4
解析:
1. 在$Rt \bigtriangleup ABC$中,已知$\angle C=90^\circ$,$AD$平分$\angle BAC$,交$BC$于点$D$,且$CD=4$。
2. 根据角平分线的性质,角平分线上的点到角的两边的距离相等。
3. 因此,点$D$到$AB$的距离等于点$D$到$AC$的距离。
4. 已知$CD$垂直于$AC$,所以$CD$的长度即为点$D$到$AC$的距离。
5. 所以点$D$到$AB$的距离等于$CD$的长度,即$4$。
2. 如图,AB= AC,∠BAC= 120°,AB的垂直平分线交BC于点D,则∠ADC=
60
°.

答案:60
解析:
因为$AB = AC$,$\angle BAC=120^{\circ}$,根据等腰三角形两底角相等以及三角形内角和为$180^{\circ}$,可得$\angle B=\angle C=\frac{180^{\circ}-\angle BAC}{2}=\frac{180 - 120}{2}=30^{\circ}$。
因为$DE$是$AB$的垂直平分线($DE$为图中垂直$AB$的直线),所以$DA = DB$,那么$\angle B=\angle BAD = 30^{\circ}$。
根据三角形的一个外角等于与它不相邻的两个内角之和,在$\triangle ABD$中,$\angle ADC=\angle B+\angle BAD$,所以$\angle ADC = 30^{\circ}+30^{\circ}=60^{\circ}$。