2. 如图,在△ABC中,D是AB中点,DE⊥AC,垂足为E,DF⊥BC,垂足为F,且ED= FD,求证:△ABC是等腰三角形.
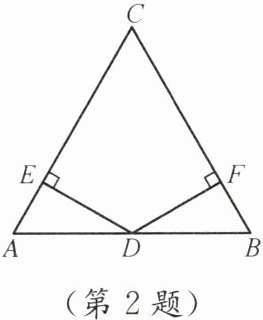
答案:证明:
因为$D$是$AB$中点,所以$AD = BD$。
因为$DE\perp AC$,$DF\perp BC$,在$Rt\triangle ADE$和$Rt\triangle BDF$中,$\left\{\begin{array}{l}AD = BD,\\DE = DF.\end{array}\right.$
根据$HL$定理,可得$Rt\triangle ADE\cong Rt\triangle BDF$,所以$AE = BF$。
设$AE = BF = x$,$CE = y$,$CF = z$。
在$Rt\triangle CDE$和$Rt\triangle CDF$中,$\left\{\begin{array}{l}DE = DF,\\CD = CD.\end{array}\right.$
根据$HL$定理,可得$Rt\triangle CDE\cong Rt\triangle CDF$,所以$CE = CF$,即$y = z$。
那么$AC=x + y$,$BC=x + z$,因为$y = z$,所以$AC = BC$。
所以$\triangle ABC$是等腰三角形。
3. (1)如图①,AD是∠BAC的平分线,CE//AB,CE交AD的延长线于点E,则
△ACE
是等腰三角形.
(2)如图②,AD是∠BAC的平分线,EF//AD,EF分别与AB,BC相交于点G,F,与CA的延长线相交于点E,则
△AGE
是等腰三角形.
(3)请从(1)(2)中选择其一加以证明.

答案:(1)△ACE;(2)△AGE
解析:
(1)∵AD平分∠BAC,∴∠BAD=∠CAD。∵CE//AB,∴∠E=∠BAD,∴∠E=∠CAD,∴AC=EC,∴△ACE是等腰三角形。
(2)∵AD平分∠BAC,∴∠BAD=∠CAD。∵EF//AD,∴∠AGE=∠BAD,∠E=∠CAD,∴∠AGE=∠E,∴AG=AE,∴△AGE是等腰三角形。
(3)选择(1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD。∵CE//AB,∴∠E=∠BAD,∴∠E=∠CAD,∴AC=EC,∴△ACE是等腰三角形。
1. 在如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两格点,C也是格点,且使得△ABC为等腰三角形,则满足条件的点C有(
D
)

A.5个
B.6个
C.7个
D.8个
答案:D
解析:
1. 如图所示,设点A的坐标为(0, 0),点B的坐标为(2, 2)。
2. 根据等腰三角形的性质,点C应满足$AC = BC$或$AC = AB$或$BC = AB$。
3. 通过观察网格,找出所有可能的格点C,使得$\triangle ABC$为等腰三角形。
4. 分别计算:
$AB = \sqrt{(2-0)^2 + (2-0)^2} = \sqrt{8} = 2\sqrt{2}$。
满足$AC = AB$的点C有:(0, 4), (4, 0)。
满足$BC = AB$的点C有:(4, 4), (0, 2)(舍去,与B在同一竖直线上),(2, 0)(舍去,与B在同一水平线上),(2, 4), (4, 2)。
满足$AC = BC$的点C有:(1, 3), (3, 1)。
5. 综合上述,符合条件的点C共有8个。