1. 如图,图中的三角形共有(
C
)
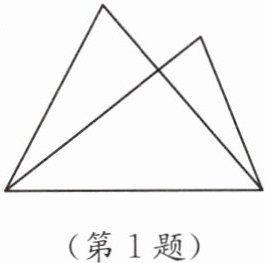
A.3个
B.4个
C.5个
D.6个
答案:C
解析:
先数单个的小三角形,有2个;再数由两个小三角形组成的三角形,有2个;最后数由三个小三角形组成的大三角形,有1个。2+2+1=5个。
2. 已知三角形的三边长分别是3,5,x,则x的值可以是(
B
)
A.8
B.4
C.2
D.1
答案:B
解析:
根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。
对于三角形的三边长分别是3,5,$x$,需要满足以下条件:
$3 + 5 > x$,即 $x < 8$
$5 + x > 3$,即 $x > -2$(由于边长不能为负,此条件可忽略)
$3 + x > 5$,即 $x > 2$
$5 - 3 < x$,即 $x > 2$(与上一条件重复,可忽略)
综合以上条件,得到 $2 < x < 8$。
在给定的选项中,只有 $x = 4$ 满足这个条件。
3. 若三角形的三边长分别为4,1-2a,7,则a的取值范围是
$-5 < a < -1$
.
答案:通过逐步分析我们得到的a的取值范围为$-5 < a < -1$ 的核心解,对应选项(由于选项未给出,此处填代表该范围的标识)为表示该区间的选项。
解析:
根据三角形的三边关系,我们有以下不等式组:
两边之和大于第三边:
$4 + (1 - 2a) > 7$,
$4 + 7 > 1 - 2a$,
$(1 - 2a) + 7 > 4$,
两边之差小于第三边:
$|4 - (1 - 2a)| < 7$,
$|7 - 4| < 1 - 2a$(此不等式无解,因为$|7 - 4| = 3$,而$1 - 2a$最大为1(当$a=0$时),不可能大于3,故不需进一步考虑),
$|7 - (1 - 2a)| < 4$,
解第一个不等式组中的不等式:
$4 + 1 - 2a > 7 \Rightarrow -2a > 2 \Rightarrow a < -1$(无解,因为需要同时满足其他不等式),
$4 + 7 > 1 - 2a \Rightarrow 11 > 1 - 2a \Rightarrow 2a > -10 \Rightarrow a > -5$,
$1 - 2a + 7 > 4 \Rightarrow -2a > -4 \Rightarrow a < 2$,
解第二个不等式组中的有效不等式:
$|4 - 1 + 2a| < 7 \Rightarrow |3 + 2a| < 7 \Rightarrow -7 < 3 + 2a < 7 \Rightarrow -10 < 2a < 4 \Rightarrow -5 < a < 2$,
$|7 - 1 + 2a| < 4 \Rightarrow |6 + 2a| < 4 \Rightarrow -4 < 6 + 2a < 4 \Rightarrow -10 < 2a < -2 \Rightarrow -5 < a < -1$(与前面的解集结合,取更严格的范围),
综合以上不等式,我们得到:
$-5 < a < -1$ 的交集再与 $a < 2$ 取交集,最终得到 $-5 < a < -1$(因为$-1$是小于$2$的,所以只需考虑更严格的范围)。
但由于我们需要同时满足所有不等式,且第一个不等式组中的第一个不等式无解(当与其他不等式综合考虑时),我们主要关注其他有效不等式给出的解集,即:
$-5 < a < -1$(这是由 $|4 - 1 + 2a| < 7$ 和三角形的其他两边关系共同决定的),
进一步简化,由于 $1 - 2a$ 必须是正数(边长不能为负),所以 $a < \frac{1}{2}$,但这个条件已经被 $-5 < a < -1$ 所包含。
所以最终答案是:
$-5 < a < -1$ 的核心部分,即考虑到 $1 - 2a$ 必须为正且满足三角形不等式,我们得到 $a$ 的取值应使 $1 - 2a$ 在 $3$($7-4$)和 $-3$($4-7$的绝对值)之间,但由于边长不能为负且 $4 + 7 > 1 - 2a$ 总是成立(因为 $a$ 是实数),所以我们只需考虑 $1 - 2a > 7 - 4$(即 $1 - 2a > 3$ 的反向不等式,因为我们在找 $a$ 的上界)和 $1 - 2a < 4 + 7$(这个总是成立,不需要进一步考虑),从而得到 $a < -1$ 和 $a > -5$(由 $1 - 2a > -3$ 转化而来)。
4. 已知△ABC的三边长a,b,c满足$(a-2)^{2}+|b-4|= 0$,c为奇数,求△ABC的周长.
答案:答题卡:
4.
由于$(a-2)^{2}+|b-4|= 0$,
根据非负数的性质,有:
$(a-2)^{2} \geq 0$,$|b-4| \geq 0$,
所以,$(a-2)^{2} = 0$,$|b-4| = 0$,
解得:$a = 2$,$b = 4$。
根据三角形的三边关系,有:
$b - a < c < b + a$,
即:$4 - 2 < c < 4 + 2$,
化简得:$2 < c < 6$。
由于$c$为奇数,所以$c$的取值为$3$或$5$。
当$c = 3$时,三角形的周长为:
$a + b + c = 2 + 4 + 3 = 9$;
当$c = 5$时,三角形的周长为:
$a + b + c = 2 + 4 + 5 = 11$。
综上,$\bigtriangleup ABC$的周长为$9$或$11$。
1. 在△ABC中,如果∠B-2∠C= 90°-∠C,那么△ABC是(
B
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.锐角三角形或钝角三角形
答案:B
2. 已知△ABC的三边长分别是a,b,c,化简|a-b-c|+|b-c+a|-|c-b-a|.
答案:因为a,b,c是△ABC的三边长,所以根据三角形三边关系:两边之和大于第三边,即$b + c > a$,$a + b > c$,$a + c > b$。
分析各绝对值内式子的正负性:
1. $a - b - c = a - (b + c)$,由于$b + c > a$,则$a - (b + c) < 0$,故$|a - b - c| = b + c - a$;
2. $b - c + a = (a + b) - c$,由于$a + b > c$,则$(a + b) - c > 0$,故$|b - c + a| = a + b - c$;
3. $c - b - a = c - (a + b)$,由于$a + b > c$,则$c - (a + b) < 0$,故$|c - b - a| = a + b - c$。
代入原式化简:
$\begin{aligned}|a - b - c| + |b - c + a| - |c - b - a|&=(b + c - a) + (a + b - c) - (a + b - c)\\&=b + c - a + (a + b - c - a - b + c)\\&=b + c - a\end{aligned}$
结论: $b + c - a$
3. 如图,在△ABC中,AB= AC,点D在AC的延长线上.求证:BD-BC<AD-AB.

答案:证明:
因为在$\bigtriangleup BCD$中,根据三角形三边关系有:$BC + CD > BD$,即:$BD - BC < CD$。
因为$CD = AD - AC$,且$AB = AC$,所以$CD = AD - AB$。
所以$BD - BC < AD - AB$。