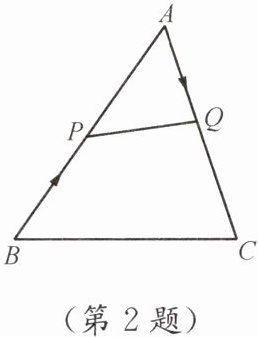
2. 如图,在△ABC中,AB= 20cm,AC= 12cm,动点P从点B出发以3cm/s的速度向点A运动,同时点Q从点A出发以2cm/s的速度向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动. 当△APQ是以∠A为顶角的等腰三角形时,运动时间是多少?
答案:设运动时间为$ t $秒。
1. 表示线段长度:
点$ P $从$ B $向$ A $运动,速度为$ 3\,cm/s $,则$ BP = 3t \,cm $,故$ AP = AB - BP = 20 - 3t \,cm $。
点$ Q $从$ A $向$ C $运动,速度为$ 2\,cm/s $,则$ AQ = 2t \,cm $。
2. 等腰三角形条件:
因$ \triangle APQ $以$ \angle A $为顶角,故$ AP = AQ $。
3. 列方程求解:
$ 20 - 3t = 2t $
解得$ 5t = 20 $,即$ t = 4 $。
4. 验证取值范围:
点$ P $运动至$ A $需$ t \leq \frac{20}{3} \approx 6.67 \,s $,点$ Q $运动至$ C $需$ t \leq 6 \,s $,$ t = 4 \,s $在$ 0 \leq t \leq 6 $范围内,符合题意。
结论:运动时间是$ 4 $秒。
$\boxed{4}$
3. 为探究等腰三角形中一腰上的高与底边所成的夹角和顶角的数量关系,小明进行了以下思考:
(1)如图①,在△ABC中,AB= AC,∠A= 50°,BD是边AC上的高,则∠DBC=
25°
;
如图②,在△ABC中,AB= AC,∠A= 90°,BD是边AC上的高,则∠DBC=
45°
;
如图③,在△ABC中,AB= AC,∠A= 120°,BD是边AC上的高,则∠DBC=
60°
.
(2)对任意的等腰三角形ABC,AB= AC,BD是边AC上的高,∠BAC与∠DBC的数量关系可能是
∠BAC = 2∠DBC
.
(3)对于上述猜想,你能证明其正确性吗?

答案:(1)
图①:
因为$AB = AC$,$\angle A=50^{\circ}$,根据等腰三角形两底角相等及三角形内角和为$180^{\circ}$,可得$\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180 - 50}{2}=65^{\circ}$。
因为$BD$是边$AC$上的高,所以$\angle BDC = 90^{\circ}$,在$\triangle BDC$中,$\angle DBC=180^{\circ}-\angle BDC-\angle C=180 - 90 - 65 = 25^{\circ}$。
图②:
因为$AB = AC$,$\angle A = 90^{\circ}$,所以$\triangle ABC$是等腰直角三角形,$\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180 - 90}{2}=45^{\circ}$。
因为$BD$是边$AC$上的高,所以$\angle BDC = 90^{\circ}$,在$\triangle BDC$中,$\angle DBC=180^{\circ}-\angle BDC-\angle C=180 - 90 - 45 = 45^{\circ}$。
图③:
因为$AB = AC$,$\angle A = 120^{\circ}$,根据等腰三角形两底角相等及三角形内角和为$180^{\circ}$,可得$\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180 - 120}{2}=30^{\circ}$。
因为$BD$是边$AC$上的高,所以$\angle BDC = 90^{\circ}$,在$\triangle BDC$中,$\angle DBC=180^{\circ}-\angle BDC-\angle C=180 - 90 - 30 = 60^{\circ}$。
(2)$\angle BAC = 2\angle DBC$
(3)
证明:
因为$AB = AC$,所以$\angle C=\frac{180^{\circ}-\angle BAC}{2}=90^{\circ}-\frac{1}{2}\angle BAC$。
因为$BD$是边$AC$上的高,所以$\angle BDC = 90^{\circ}$。
在$\triangle BDC$中,$\angle DBC=180^{\circ}-\angle BDC-\angle C=180 - 90-(90^{\circ}-\frac{1}{2}\angle BAC)=\frac{1}{2}\angle BAC$。
即$\angle BAC = 2\angle DBC$。
综上,答案依次为:(1)$25^{\circ}$;$45^{\circ}$;$60^{\circ}$;(2)$\angle BAC = 2\angle DBC$;(3)证明过程如上述。