2. 如图,OC平分∠AOB,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,若∠DOP= 20°,则∠OPE=
70
°;若PD= 1,则PE=
1
.
答案:70;1
解析:
1. 由于OC平分∠AOB,且点P在OC上,因此∠AOP = ∠BOP。
2. PD垂直于OA,PE垂直于OB,因此∠PDO = ∠PEO = 90°。
3. 在△ODP和△OEP中,由于∠AOP = ∠BOP,∠PDO = ∠PEO = 90°,且OP是公共边,所以△ODP ≅ △OEP(AAS)。
4. 因此,PD = PE,且∠OPD = ∠OPE。
5. 已知∠DOP = 20°,所以∠OPE = 90° - ∠DOP = 90° - 20° = 70°。
6. 由于PD = 1,因此PE = 1。
3. 如图,OP平分∠MON,PA⊥ON,垂足为A,Q是射线OM上的一个动点,若PA= 2,则线段PQ的最小值为
2
.
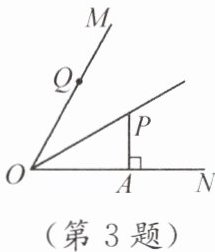
答案:2
解析:
1. 由题意可知,OP平分∠MON,PA⊥ON,且PA=2。
2. 根据角平分线的性质,角平分线上的点到角的两边的距离相等,所以P到OM的距离等于PA,即2。
3. 因为Q是OM上的动点,PQ的长度会随着Q的位置变化而变化。
4. 当PQ垂直于OM时,PQ的长度最短,此时PQ的长度等于P到OM的距离,即2。
4. 如图,已知∠ABC,D是∠ABC的平分线上的一点,点E,F分别在AB,BC上,且DE= DF.试判断∠BED与∠BFD的关系,并说明理由.

答案:∠BED=∠BFD.
理由如下:
过点D作DM⊥AB于M,DN⊥BC于N.
∵D是∠ABC平分线上的点,
∴DM=DN(角平分线上的点到角两边的距离相等).
在Rt△DME和Rt△DNF中,
∵DE=DF,DM=DN,
∴Rt△DME≌Rt△DNF(HL).
∴∠DEM=∠DFN.
∵DM⊥AB,DN⊥BC,
∴∠DEM=∠BED,∠DFN=∠BFD.
∴∠BED=∠BFD.
1. 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.已知△ABC的面积为7,DE= 2,AB= 4,则AC的长是______
3
.

答案:3
解析:
因为$AD$是$\angle BAC$的平分线,$DE\perp AB$,$DF\perp AC$,根据角平分线的性质可知$DE = DF$。
已知$DE = 2$,所以$DF = 2$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),$\triangle ABC$的面积$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$。
$S_{\triangle ABD}=\frac{1}{2}× AB× DE$,$S_{\triangle ACD}=\frac{1}{2}× AC× DF$。
已知$S_{\triangle ABC}=7$,$AB = 4$,$DE = DF = 2$,则$\frac{1}{2}×4×2+\frac{1}{2}× AC×2=7$。
即$4 + AC=7$,解得$AC = 3$。
2. 已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.
求证:AD垂直平分EF.

答案:证明:
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF(角平分线上的点到角两边距离相等)。
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°。
在△AED和△AFD中,
∠EAD=∠FAD(AD是角平分线),
∠AED=∠AFD,
AD=AD(公共边),
∴△AED≌△AFD(AAS)。
∴AE=AF,DE=DF。
∵AE=AF,
∴点A在EF的垂直平分线上(到线段两端距离相等的点在垂直平分线上)。
∵DE=DF,
∴点D在EF的垂直平分线上。
∵点A、D在EF的垂直平分线上,
∴AD垂直平分EF(两点确定一条直线)。