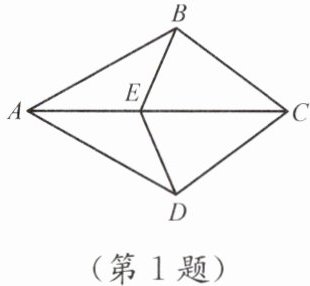
1. 如图,AB= AD,BC= CD,则全等三角形共有 (
C
)
A.1对
B.2对
C.3对
D.4对
答案:C
解析:
在$\bigtriangleup ABC$和$\bigtriangleup ADC$中,
$\begin{cases}AB = AD,\\BC = CD,\\AC = AC.\end{cases}$
根据“边边边”($SSS$)判定定理,可得$\bigtriangleup ABC\cong\bigtriangleup ADC$。
因为$\bigtriangleup ABC\cong\bigtriangleup ADC$,所以$\angle BAE=\angle DAE$,$\angle ABE = \angle ADE$。
在$\bigtriangleup ABE$和$\bigtriangleup ADE$中,
$\begin{cases}AB = AD,\\\angle BAE=\angle DAE,\\AE = AE.\end{cases}$
根据“边角边”($SAS$)判定定理,可得$\bigtriangleup ABE\cong\bigtriangleup ADE$。
因为$\bigtriangleup ABC\cong\bigtriangleup ADC$,所以$\angle BCE=\angle DCE$。
在$\bigtriangleup BCE$和$\bigtriangleup DCE$中,
$\begin{cases}BC = CD,\\\angle BCE=\angle DCE,\\CE = CE.\end{cases}$
根据“边角边”($SAS$)判定定理,可得$\bigtriangleup BCE\cong\bigtriangleup DCE$。
所以全等三角形有$\bigtriangleup ABC\cong\bigtriangleup ADC$,$\bigtriangleup ABE\cong\bigtriangleup ADE$,$\bigtriangleup BCE\cong\bigtriangleup DCE$,共$3$对。
2. 如图,在下列条件中,不能直接判定△ABC与△DCB全等的是 (
B
)

A.AB= CD,BD= CA
B.∠A= ∠D,AB= DC
C.∠A= ∠D,∠ACB= ∠DBC
D.AB= DC,∠ABC= ∠DCB
答案:B
解析:
A.由$AB = CD$,$BD = CA$ 以及$BC=CB$,可根据$SSS$判定$\triangle ABC\cong\triangle DCB$。
B.由$\angle A=\angle D$,$AB = DC$以及$BC = CB$,是$SSA$,不能判定$\triangle ABC\cong\triangle DCB$。
C.由$\angle A=\angle D$,$\angle ACB=\angle DBC$以及$BC = CB$,可根据$AAS$判定$\triangle ABC\cong\triangle DCB$。
D.由$AB = DC$,$\angle ABC=\angle DCB$以及$BC = CB$,可根据$SAS$判定$\triangle ABC\cong\triangle DCB$。
3. 如图,用直尺和圆规作一个角的平分线,由作图步骤判定∠BOC= ∠AOC的过程中用到了 (
D
)

A.SAS
B.ASA
C.AAS
D.SSS
答案:D
解析:
用直尺和圆规作角平分线时,以O为圆心画弧,分别交OA、OB于点A、B,再分别以A、B为圆心,大于1/2AB长为半径画弧,两弧交于点C,连接OC。则OA=OB,AC=BC,OC=OC,根据SSS可证△AOC≌△BOC,所以∠BOC=∠AOC。
4. 如图,点B,D,C在同一条直线上,AB= AD,BC= DE,AC= AE.
(1)求证:∠CAE= ∠BAD.
(2)已知∠BAD= 42°,求∠CDE的大小.

答案:(1)见解析;(2)42°
解析:
(1)在△ABC和△ADE中,
∵AB=AD,AC=AE,BC=DE,
∴△ABC≌△ADE(SSS),
∴∠BAC=∠DAE,
∵∠BAC=∠BAD+∠DAC,∠DAE=∠CAE+∠DAC,
∴∠BAD+∠DAC=∠CAE+∠DAC,
∴∠CAE=∠BAD.
(2)∵AB=AD,∠BAD=42°,
∴∠ABD=∠ADB=(180°-42°)/2=69°,
∵点B,D,C在同一直线上,
∴∠ADC=180°-∠ADB=180°-69°=111°,
∵△ABC≌△ADE,
∴∠ADE=∠ABC=∠ABD=69°,
∴∠CDE=∠ADC-∠ADE=111°-69°=42°.
1. 下列各组条件中,能判定△ABC≌△DEF的是 (
C
)
A.AB= DE,BC= EF,∠A= ∠D
B.∠A= ∠D,∠C= ∠F,AC= EF
C.AB= DE,BC= EF,△ABC的周长等于△DEF的周长
D.∠A= ∠D,∠B= ∠E,∠C= ∠F
答案:C
解析:
A选项:给出了两边及一边的对角相等,即AB=DE,BC=EF,∠A=∠D。这不符合全等三角形的任何判定定理,故A错误。
B选项:给出了两角及一边,但这一边并不是两角的夹边,即∠A=∠D,∠C=∠F,AC=EF。这也不符合全等三角形的判定定理,故B错误。
C选项:给出了两条边相等,即AB=DE,BC=EF,并且两个三角形的周长也相等。由周长相等,我们可以推出第三条边也相等,即AC=DF。这符合SSS(三边相等)的全等判定条件,故C正确。
D选项:只给出了三个角相等,即∠A=∠D,∠B=∠E,∠C=∠F。没有边的信息,所以不能判定两个三角形全等,故D错误。
2. 已知:如图,AB= DC,DB= AC.
求证:∠ABD= ∠DCA.

答案:证明:
连接$BC$。
在$\triangle ABC$和$\triangle DCB$中:
$AB = DC$,$AC = DB$,$BC = CB$(公共边)。
根据“边边边”(SSS)全等判定定理,可得$\triangle ABC\cong\triangle DCB$。
所以$\angle ABC = \angle DCB$,$\angle ACB = \angle DBC$。
因为$\angle ABD=\angle ABC - \angle DBC$,$\angle DCA=\angle DCB - \angle ACB$,所以$\angle ABD = \angle DCA$。