2025年伴你学八年级数学上册苏科版第140页解析答案

27. (14分)【发现问题】
因为$(a-b)^{2}\geq 0$,所以$a^{2}+b^{2}\geq 2ab$,由此可得:若$a＞0,b＞0$,则有不等式$a+b\geq 2\sqrt{ab}$,当且仅当$a= b$时取等号.
【提出问题】
若$a＞0,b＞0$,能否求出$a+b$的最小值呢?
【分析问题】
例:已知$x＞0$,求式子$x+\frac{4}{x}$的最小值.
解:令$a= x,b= \frac{4}{x}$,由$a+b\geq 2\sqrt{ab}$,得$x+\frac{4}{x}\geq 2\sqrt{x\cdot \frac{4}{x}}= 4$.当且仅当$x= \frac{4}{x}$,即$x= 2$时,式子有最小值,最小值为4.
【解决问题】
请根据上面材料回答下列问题:
(1) 比较大小:$2+3$

＞

$2\sqrt{2× 3}$;当$x＞0$时,式子$x+\frac{1}{x}$的最小值为

.
【能力提升】
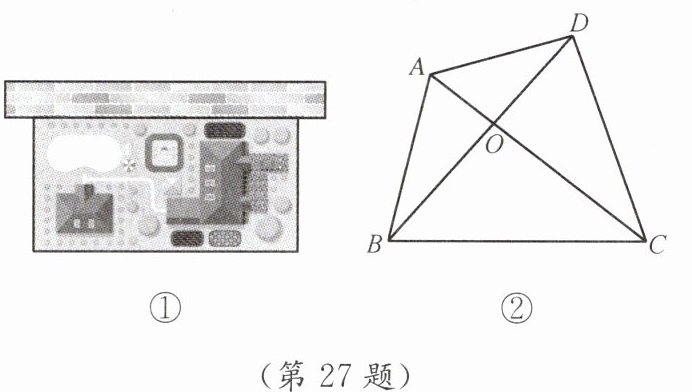
(2) 如图①,用篱笆围一个面积为$32\ m^{2}$的长方形花园,该长方形花园的一边靠墙,墙长20 m,该长方形花园的长、宽各为多少米时,所用的篱笆最短？最短的篱笆是多少?

当长方形花园的长为8米，宽为4米时，所用的篱笆最短，最短的篱笆是16米。

(3) 如图②,四边形ABCD的对角线AC,BD相交于点O,$\triangle AOB$,$\triangle COD$的面积分别是8和14,求四边形ABCD面积的最小值.

四边形ABCD面积的最小值为$22 + 8\sqrt{7}$。

答案：(1) $2 + 3 = 5$，$2\sqrt{2 × 3} = 2\sqrt{6} \approx 4.899$，所以$2 + 3 ＞ 2\sqrt{2 × 3}$。
令$a = x$，$b = \frac{1}{x}$，由$a + b \geq 2\sqrt{ab}$，得$x + \frac{1}{x} \geq 2\sqrt{x \cdot \frac{1}{x}} = 2$，当且仅当$x = \frac{1}{x}$，即$x = 1$时，式子有最小值，最小值为$2$。
故答案为：$＞$；$2$。
(2) 设长方形花园的宽为$x$米，长为$y$米。
由已知$xy = 32$，$y \leq 20$，篱笆长$L = 2x + y$。
由$xy = 32$，得$y = \frac{32}{x}$，则$L = 2x + \frac{32}{x}$。
令$a = 2x$，$b = \frac{32}{x}$，由$a + b \geq 2\sqrt{ab}$，得$2x + \frac{32}{x} \geq 2\sqrt{2x \cdot \frac{32}{x}} = 16$，当且仅当$2x = \frac{32}{x}$，即$x = 4$时，$L$有最小值$16$，此时$y = 8$。
所以，当长方形花园的长为$8$米，宽为$4$米时，所用的篱笆最短，最短的篱笆是$16$米。
(3) 设$\triangle AOD$的面积为$x$，$\triangle BOC$的面积为$y$。
由$\triangle AOB$与$\triangle AOD$同高，面积比等于底边比，得$\frac{S_{\triangle AOB}}{S_{\triangle AOD}} = \frac{BO}{OD}$，即$\frac{8}{x} = \frac{BO}{OD}$。
同理，$\frac{S_{\triangle BOC}}{S_{\triangle COD}} = \frac{BO}{OD}$，即$\frac{y}{14} = \frac{BO}{OD}$。
所以$\frac{8}{x} = \frac{y}{14}$，即$xy = 112$。
四边形$ABCD$的面积$S = 8 + 14 + x + y = 22 + x + y$。
令$a = x$，$b = y$，由$a + b \geq 2\sqrt{ab}$，得$x + y \geq 2\sqrt{xy} = 2\sqrt{112} = 8\sqrt{7}$，当且仅当$x = y$时取等号。
所以$S = 22 + x + y \geq 22 + 8\sqrt{7}$，当且仅当$x = y = 4\sqrt{7}$时，$S$有最小值$22 + 8\sqrt{7}$。
故四边形$ABCD$面积的最小值为$22 + 8\sqrt{7}$。