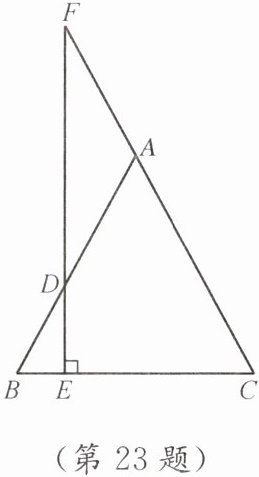
23. (10分)如图,在$\triangle ABC$中,$AB= AC$,D是边AB上一点,过点D作$DE\perp BC$,垂足为E,交CA的延长线于点F.
(1) 求证:$AD= AF$;
(2) 若$\angle B= 2\angle F$,$BE= 2$,$CF= 16$,求BC的长.
答案:(1) 见解析;(2) 10。
解析:
(1) 证明:
∵AB=AC,∴∠B=∠C。
∵DE⊥BC,∴∠DEB=∠DEC=90°。
在Rt△DEB中,∠B+∠BDE=90°;在Rt△FEC中,∠C+∠F=90°。
∵∠B=∠C,∴∠BDE=∠F。
∵∠BDE=∠ADF(对顶角相等),∴∠ADF=∠F。
∴AD=AF。
(2) 设∠F=α,则∠B=2α。
由(1)知∠BDE=∠F=α,在Rt△DEB中,∠B+∠BDE=90°,即2α+α=90°,解得α=30°。
∴∠F=30°,∠B=60°,∵AB=AC,∴∠C=∠B=60°,∴∠BAC=60°,△ABC为等腰三角形(AB=AC)。
设AB=AC=x,AD=AF=y,∵CF=AC+AF=16,∴x+y=16。
∵DB=AB-AD=x-y,在Rt△DEB中,∠B=60°,BE=2,cos∠B=BE/DB,即cos60°=2/DB,∴DB=4,即x-y=4。
联立{x+y=16, x-y=4},解得x=10,y=6。
∵∠B=∠C=60°,∠DEB=∠FEC=90°,∴△DEB∽△FEC。
∴BE/EC=DB/FC,即2/EC=4/16,解得EC=8。
∴BC=BE+EC=2+8=10。
24. (10分)如图,$\angle ACB= 90^{\circ},AC= BC,BE\perp CE,AD\perp CE$,垂足分别为E,D,$AD= 2.5$,$DE= 1.7$,求BE的长.

答案:$\because\angle ACB=90^\circ,BE\perp CE,AD\perp CE$,
$\therefore \angle BEC=\angle CDA=90^\circ$,
$\angle BCE+\angle ACD=90^\circ,\angle CAD+\angle ACD=90^\circ$,
$\therefore \angle BCE=\angle CAD$。
在$\triangle BCE$和$\triangle CAD$中,
$\begin{cases}\angle BEC=\angle CDA,\\\angle BCE=\angle CAD,\\BC=AC.\end{cases}$
$\therefore \triangle BCE\cong\triangle CAD(AAS)$,
$\therefore BE=CD,CE=AD=2.5$,
$\therefore BE=CD=CE-DE=2.5-1.7=0.8$。
故答案为$0.8$。