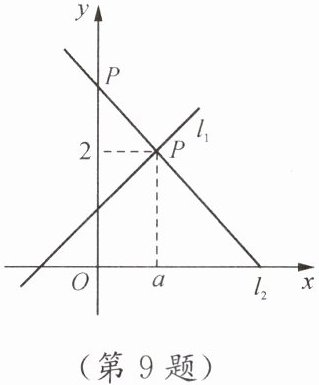
9. 如图,一次函数$y= x+1的图象与一次函数y= mx+n的图象相交于点P(a,2)$,则关于x的不等式$x+1\geq mx+n$的解集为(
D
)
A.$x\leq 1$
B.$x<1$
C.$x>1$
D.$x\geq 1$
答案:D
解析:
将点$P(a,2)$代入$y=x+1$得:$a+1=2$,解得$a=1$。
所以点$P$的坐标为$(1,2)$。
观察图象可知,当$x\geq 1$时,直线$y=x+1$落在直线$y=mx+n$上方,即$x+1\geq mx+n$。
所以不等式$x+1\geq mx+n$的解集为$x\geq 1$。
10. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ},\angle A= 30^{\circ},BC= 2$,将$\triangle ABC$绕点C按顺时针方向旋转$n^{\circ}$后,得到$\triangle EDC$,此时,点D在边AB上,斜边DE交边AC于点F,则n的值和图中阴影部分的面积分别为(
C
)

A.30,2
B.60,2
C.$60,\frac{\sqrt{3}}{2}$
D.$60,\sqrt{3}$
答案:C
解析:
在$Rt\triangle ABC$中,$\angle A=30^\circ$,$\angle ACB=90^\circ$,$BC=2$,则$AB=4$(30°角所对直角边是斜边一半),$AC=2\sqrt{3}$(勾股定理)。
旋转后$CD=CB=2$,点$D$在$AB$上,$\triangle CBD$中$CB=CD=DB=2$($DB=AB-AD=4-2=2$),故$\triangle CBD$为等边三角形,旋转角$n=\angle BCD=60^\circ$。
$\angle ACD=90^\circ-60^\circ=30^\circ$,在$\triangle DFC$中,$\angle FDC=60^\circ$(对应$\angle B$),$\angle DCF=30^\circ$,则$\angle DFC=90^\circ$。
$CD=2$,$DF=CD\cdot\sin30^\circ=1$,$CF=CD\cdot\cos30^\circ=\sqrt{3}$,阴影面积$S_{\triangle DFC}=\frac{1}{2}× DF× CF=\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{2}$。
11. 若$x^{3}= -8$,则$x= $
$-2$
.
答案:$x = - 2$(这里按要求应填对应序号,若题目是填空题形式,答案就写$-2$ )
解析:
给定$x^{3} = -8$,根据立方根的定义,若$a^{3}=b$,则$a$是$b$的立方根,记作$a=\sqrt[3]{b}$。所以$x=\sqrt[3]{-8}$,因为$( - 2)^{3}=-8$,所以$x=-2$。
12. $\sqrt{3}-2$的绝对值是
$2-\sqrt{3}$
.
答案:由于本题为填空题,故答案为$2-\sqrt{3}$
解析:
首先,需要确定$\sqrt{3}-2$的符号。
由于$\sqrt{3}$的值约等于1.732,小于2,所以$\sqrt{3}-2$的值小于0。
根据绝对值的定义,一个负数的绝对值等于它的相反数。
因此,$|\sqrt{3}-2|$等于$-(\sqrt{3}-2)$,即$2-\sqrt{3}$。
13. 已知一个正数的两个平方根分别是$2a-2$和$a-4$,则$a$的值是
2
.
答案:2
解析:
已知一个正数的两个平方根分别是 $2a-2$ 和 $a-4$,根据平方根的性质,一个正数的两个平方根互为相反数,即和为0。
所以有:
$2a - 2 + a - 4 = 0$
整理得:
$3a - 6 = 0$
进一步解得:
$a = 2$
14. 已知点$A(a,-2)与B(5,b)$关于x轴对称,则$a+b= $
7
.
答案:7
解析:
由于点$A(a, -2)$和点$B(5, b)$关于$x$轴对称,根据对称性质,两点的横坐标相同,纵坐标互为相反数。
因此,有$a = 5$,$b = -(-2) = 2$。
所以,$a + b = 5 + 2 = 7$。
15. 如图是一个围棋棋盘(局部),若把这个围棋棋盘放置在平面直角坐标系中,白棋①的坐标是$(-1,-2)$,白棋③的坐标是$(0,-4)$,则黑棋②的坐标是
$(1, -3)$
.

答案:$(1, -3)$
解析:
1. 确定白棋①的坐标为$(-1, -2)$,白棋③的坐标为$(0, -4)$。
2. 观察棋盘,确定黑棋②的位置。
3. 根据棋盘上的位置,黑棋②位于白棋③的右上方一格,即横坐标增加1,纵坐标增加1。
4. 因此,黑棋②的坐标为$(0+1, -4+1) = (1, -3)$。
16. 如图,在等边三角形ABC中,$BD= CE$,AD与BE相交于点P,则$\angle APE$的度数是______
60°
.

答案:60°
解析:
因为$\triangle ABC$是等边三角形,所以$AB=BC$,$\angle ABC=\angle C=60^\circ$。
又因为$BD=CE$,所以$\triangle ABD\cong\triangle BCE(SAS)$。
所以$\angle BAD=\angle CBE$。
因为$\angle APE$是$\triangle ABP$的外角,所以$\angle APE=\angle BAD+\angle ABE$。
所以$\angle APE=\angle CBE+\angle ABE=\angle ABC=60^\circ$。
17. 将一根长为24 cm的筷子置于底面直径为5 cm、高为12 cm的圆柱形空水杯中,则筷子露出杯子外面的长度最短为
11
cm.
答案:11
解析:
要使筷子露出杯子外面的长度最短,则筷子在杯子内的长度应最长,即当筷子在杯内构成一个直角三角形的斜边时,其在杯内的长度最长。
设筷子在杯内的长度为$x$ cm,根据勾股定理,有:
$x^2 = 12^2 + 5^2$
$x^2 = 144 + 25$
$x^2 = 169$
解得:$x = 13$ (负值舍去,因为长度不能为负)
所以,筷子露出杯子外面的长度最短为:
$24 - 13 = 11$ cm
18. 已知一次函数$y= ax+b$($a,b$是常数),x与y的部分对应值如下表:
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |

方程$ax+b= 0$的解是______
$x=1$
.
答案:$x=1$
解析:
由表可知,当$x=1$时,$y=0$,即$ax+b=0$,所以方程$ax+b=0$的解是$x=1$。