1. 若点P(m+3,m+1)在x轴上,则点P的坐标为 (
D
)
A.(0,-4)
B.(4,0)
C.(0,-2)
D.(2,0)
答案:D
解析:
由于点$P(m+3, m+1)$在$x$轴上,根据$x$轴的性质,其$y$坐标必须为0。
因此,我们有:
$m + 1 = 0$
解这个方程,我们得到:
$m = -1$
将$m = -1$代入点$P$的$x$坐标表达式$m+3$,我们得到:
$m + 3 = -1 + 3 = 2$
因此,点$P$的坐标为$(2, 0)$。
2. 若点B在y轴上且到点A(0,4)的线段长度为5,则点B的坐标为 (
C
)
A.(0,9)
B.(0,-1)
C.(0,9)或(0,-1)
D.(9,0)或(-1,0)
答案:C
解析:
因为点B在y轴上,所以点B的横坐标为0。设点B的坐标为$(0, y)$。根据两点间的距离公式,点B到点A$(0, 4)$的距离为$\sqrt{(0-0)^2 + (y-4)^2} = 5$。即$(y-4)^2 = 25$,解得$y-4 = 5$或$y-4 = -5$,所以$y = 9$或$y = -1$。因此,点B的坐标为$(0, 9)$或$(0, -1)$。
3. 若点P在第四象限,且到x轴的距离为3,到y轴的距离为2,则点P的坐标为 (
B
)
A.(-2,3)
B.(2,-3)
C.(3,2)
D.(-3,2)
答案:B
解析:
由于点P在第四象限,根据第四象限的坐标特性,横坐标为正,纵坐标为负。点P到x轴的距离为3,即纵坐标的绝对值为3,由于是在第四象限,所以纵坐标为-3。点P到y轴的距离为2,即横坐标的绝对值为2,由于是在第四象限,所以横坐标为2。因此,点P的坐标为(2, -3)。
4. 如图,图①中的△ABC经过一定的运动变化得到图②中的△A'B'C'.如果图①中△ABC上的点P的坐标为(a,b),那么这个点在图②中的对应点P'的坐标为 (
C
)
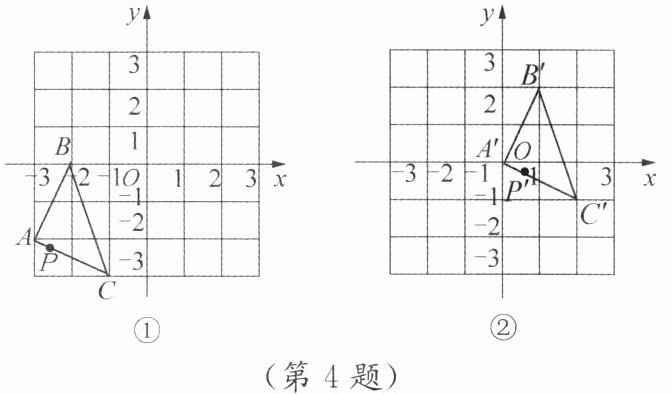
A.(a-2,b-3)
B.(a-3,b-2)
C.(a+3,b+2)
D.(a+2,b+3)
答案:C
解析:
首先,观察图①和图②中的坐标变化。
图①中的点$P(a, b)$在图②中的对应点$P'$的坐标变化可以通过观察图①和图②中三角形的平移来确定。
从图①到图②,三角形整体向右平移了3个单位,向上平移了2个单位。
因此,点$P(a, b)$在图②中的对应点$P'$的坐标应为$(a+3, b+2)$。
5. 如图,在平面直角坐标系中,点A,B的坐标分别为(1,4),(3,0),C是y轴上的一个动点,且A,B,C三点不在同一条直线上.当△ABC的周长最小时,点C的坐标为 (
D
)

A.(0,0)
B.(0,1)
C.(0,2)
D.(0,3)
答案:D
解析:
1. 根据题意,点A的坐标为(1,4),点B的坐标为(3,0)。
2. 先求出点A关于y轴的对称点A'的坐标。点A(1,4)关于y轴的对称点A'的坐标为(-1,4)。
3. 连接A'和B,交y轴于点C,此时△ABC的周长最小。
4. 设直线A'B的解析式为y=kx+b。
5. 把A'(-1,4),B(3,0)代入解析式,得到方程组:
$\begin{cases}-k+b=4 \\ 3k+b=0\end{cases}$
6. 解方程组:
用第一个方程减去第二个方程:$(-k+b)-(3k+b)=4-0$,得到$-4k=4$,解得$k=-1$。
把$k=-1$代入$-k+b=4$,得到$1+b=4$,解得$b=3$。
7. 所以直线A'B的解析式为$y=-x+3$。
8. 令$x=0$,则$y=3$,所以点C的坐标为(0,3)。
答案:四
解析:
首先,我们需要确定点$P$的横坐标$a^2+1$的符号。
由于$a^2$是非负的,所以$a^2+1$一定大于0,即$a^2+1 \gt 0$。
接着,我们观察点$P$的纵坐标,为$-3$,显然$-3 \lt 0$。
因此,点$P$的横坐标为正,纵坐标为负,所以点$P(a^2+1,-3)$位于第四象限。
7. 点P(-2,-3)关于y轴对称的点的坐标为
(2,-3)
.
答案:(2,-3)
解析:
在平面直角坐标系中,关于y轴对称的点,其横坐标互为相反数,纵坐标保持不变。
设点P(-2,-3)关于y轴对称的点为P',则P'的横坐标为-(-2)=2,纵坐标仍为-3。
所以,P'的坐标为(2,-3)。
8. 在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是
-2或8
。
答案:【解析】:
由于点$M(1, x)$和点$N(1, 3)$的横坐标相同,即$x_1 = x_2 = 1$,所以$MN$之间的距离等于两点纵坐标之差的绝对值,即
$|x - 3| = 5$
解这个绝对值方程,我们得到两个方程:
$x - 3 = 5 \quad 或 \quad x - 3 = -5$
解第一个方程得:$x = 8$
解第二个方程得:$x = -2$
所以$x$的值可以是$-2$或$8$。
【答案】:由于本题为填空题,无选项,故直接写答案:$-2$或$8$。
解析:
由于点$M(1, x)$和点$N(1, 3)$的横坐标相同,即$x_1 = x_2 = 1$,所以$MN$与$y$轴平行。
两点间的距离公式在$x$坐标相同的情况下可以简化为$|x_2 - x_1| = |y_2 - y_1|$,即$|x - 3| = 5$。
解这个绝对值方程,我们得到两个$x - 3 = 5$ 或 $x - 3 = -5$。
解得 $x = 8$ 或 $x = -2$。
9. 已知点P(m-2,1-n).
(1)如果m>2,n<1,那么点P在第
一
象限;
(2)如果n= 1,那么点P在
x
轴上;
(3)点P关于原点对称的点是
(2-m, n-1)
.
答案:(1) 一
(2) $x$
(3) $(2-m, n-1)$
解析:
(1) 根据题目条件,如果 $m > 2$,则 $m - 2 > 0$;如果 $n < 1$,则 $1 - n > 0$。由于点 $P$ 的横纵坐标都大于0,所以点 $P$ 在第一象限。
(2) 如果 $n = 1$,则 $1 - n = 0$,即点 $P$ 的纵坐标为0,所以点 $P$ 在 $x$ 轴上。
(3) 点 $P(m-2, 1-n)$ 关于原点对称的点,其横坐标和纵坐标都要取反,即对称点的坐标为 $(2-m, n-1)$。
10. 已知点A(0,-3)、B(0,-4),点C在x轴上,若△ABC的面积为15,则点C的坐标为
(30, 0)或(-30, 0)
.
答案:点$C$的坐标为$(30, 0)$或$(-30, 0)$。
解析:
由于点$A(0,-3)$,$B(0,-4)$在$y$轴上,
所以$AB$的长度为$|-3 - (-4)| = 1$,
设点$C$的坐标为$(x, 0)$,
则点$C$到$AB$(即$y$轴)的距离为$|x|$,
这一距离也是$\triangle ABC$的高,
根据三角形面积公式$S = \frac{1}{2} × 底 × 高$,
有$S_{\triangle ABC} = \frac{1}{2} × 1 × |x| = 15$,
解得$|x| = 30$,
由于$x$可以是正数或负数,
因此$x = \pm 30$,
所以点$C$的坐标为$(30, 0)$或$(-30, 0)$。
11. 如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA= 2,AB= 1,若将△OAB绕点O按顺时针方向旋转90°,则点B的对应点的坐标是
(2, -1)
.

答案:(2, -1)
解析:
1. 确定点B的坐标:由于OA=2,AB=1,且点B在第一象限,因此点B的坐标为(1, 2)。
2. 将△OAB绕点O按顺时针方向旋转90°,相当于将点B的坐标(1, 2)绕原点O顺时针旋转90°。
3. 旋转90°后的坐标变换公式为:若点(x, y)绕原点顺时针旋转90°,则新坐标为(y, -x)。
4. 将点B的坐标(1, 2)代入公式,得到新坐标为(2, -1)。