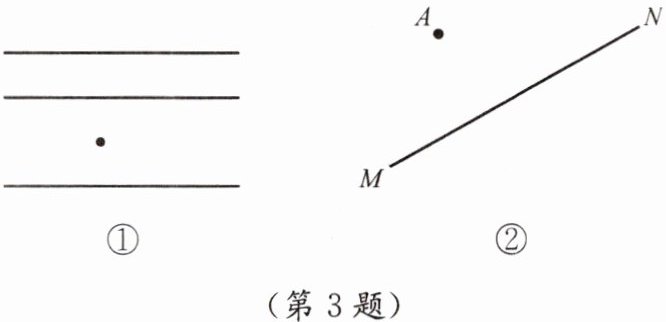
3. (1)如图①,马路上的斑马线中有一条看不清了,只能看到上面的一个点,请你将这条线画出来,依据是______.
(2)如图②,一辆汽车在公路 MN 上行驶,在哪个位置时对公路旁房屋 A 的影响最大?在图②中画出来,并说明依据.
答案:
(1)
过已知点作已知直线的平行线,依据是:经过直线外一点,有且只有一条直线与这条直线平行。
画图:用直尺和三角板,通过平移三角板的方法过该点画出已知直线的平行线。
(2)
过点$A$作$AB\perp MN$,垂足为$B$,点$B$处汽车对房屋$A$的影响最大。依据是:垂线段最短。
画图:用三角板的一条直角边与直线$MN$重合,沿直线$MN$移动三角板,使另一条直角边经过点$A$,沿这条直角边画直线,与$MN$交于点$B$。
4. 如图,线段 AB= 4,延长线段 AB 到点 C,使 BC= 1,再反向延长 AB 到点 D,使 AD= 3,E 是 AD 的中点,F 是 CD 的中点,求 CD 和 EF 的长度.

答案:$CD=AD + AB + BC=3 + 4+1 = 8$。
因为$E$是$AD$的中点,所以$AE = DE=\frac{1}{2}AD=\frac{3}{2}$。
$DF=\frac{1}{2}CD = 4$,$AF=DF - AD=4 - 3 = 1$。
$EF=DE + AF= \frac{3}{2}+1=\frac{5}{2}$。
综上,$CD$的长度为$8$,$EF$的长度为$\frac{5}{2}$。
5. 如图,已知 CD//AB,∠DCB= 70°,∠CBF= 20°,∠EFB= 130°,直线 EF 与 AB 有怎样的位置关系?请说明理由.

答案:$EF// AB$。
理由如下:
$\because CD// AB$,$\angle DCB = 70^{\circ}$,
$\therefore \angle ABC=\angle DCB = 70^{\circ}$。
$\because \angle CBF = 20^{\circ}$,
$\therefore \angle ABF=\angle ABC - \angle CBF=70^{\circ}-20^{\circ}=50^{\circ}$。
$\because \angle EFB = 130^{\circ}$,
$\therefore \angle ABF+\angle EFB=50^{\circ}+130^{\circ}=180^{\circ}$。
根据同旁内角互补,两直线平行,可得$EF// AB$。
1. 利用一副三角板,不能画出的角是(
D
)
A.15°
B.135°
C.165°
D.100°
答案:D
解析:
一副三角板的角度有30°、45°、60°、90°。
15°=45°-30°,可画出;
135°=90°+45°,可画出;
165°=90°+45°+30°,可画出;
100°无法用上述角度通过加减得到,不能画出。
D
2. 已知点 C 在线段 AB 上,且 AC= CB,延长 BA 到点 D,使 AD= AB.当 AB= 4 时,则 DB=
8
,CD=
6
.
答案:DB=8,CD=6(本题为填空题,无选项)
解析:
因为点$C$在线段$AB$上,且$AC = CB$,$AB = 4$,所以$AC=CB=\frac{AB}{2}=\frac{4}{2}=2$。
延长$BA$到点$D$,使$AD = AB = 4$,则$DB=DA + AB=4 + 4=8$。
$CD=DA + AC=4 + 2=6$。
DB=8,CD=6