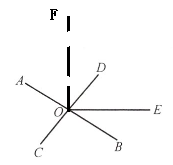
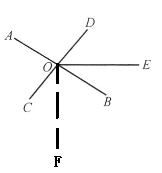
2. 下列说法中不正确的是 (
D
)
A.在同一平面内,经过一点能且只能画一条直线与已知直线垂直
B.一条线段有无数条垂线
C.在同一平面内,过射线的端点只能画一条直线与这条射线垂直
D.如果直线AB垂直平分线段CD,那么CD也垂直平分AB
答案:D
解析:
A. 根据垂线的性质,我们知道在同一平面内,经过一点有且只有一条直线与已知直线垂直,所以选项A是正确的。
B. 对于一条线段,我们可以在线段的任意位置作垂线,因此一条线段有无数条垂线,所以选项B也是正确的。
C. 对于射线,过射线的端点,我们只能画出一条与射线垂直的直线,所以选项C是正确的。
D. 如果直线AB垂直平分线段CD,这意味着AB与CD垂直,并且AB平分CD。但这并不意味着CD也垂直平分AB,因为CD可能并不平分AB,所以选项D是不正确的。
3. 如图,$OC\perp AB$,垂足为O,OD平分$\angle BOC$,求$\angle AOD$的大小.
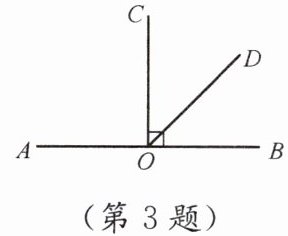
答案:解:易知,∠AOC=∠BOC=90°
∵OD平分∠BOC,∴$∠BOD=∠COD=\frac {1}{2}∠BOC=45°$
∴∠AOD=∠AOC+∠COD=135°
4. 如图,$CD\perp AB$,垂足为C,$\angle 1= 130^\circ$,求$\angle 2$的大小.

答案:解:易知,∠ACD+∠2=∠1=130°
∴∠2=130°-∠ACD=40°
1. 如图,直线AB,CD相交于点O,OE平分$\angle AOD$,$OF\perp OE$,若$\angle BOC= 80^\circ$,则$\angle DOF$的大小是 (
C
)

A.$100^\circ$
B.$120^\circ$
C.$130^\circ$
D.$115^\circ$
答案:C
解析:
∵直线AB,CD相交于点O,
∴∠AOD=∠BOC=80°(对顶角相等)。
∵OE平分∠AOD,
∴∠DOE=$\frac{1}{2}$∠AOD=$\frac{1}{2}×80^\circ=40^\circ$。
∵OF⊥OE,
∴∠EOF=90°。
∵点D,O,C在同一直线上,
∴∠DOC=180°,
∴∠DOF=∠DOC-∠EOF-∠COE。
又
∵∠COE=∠DOE=40°(对顶角相等),
∴∠DOF=180°-90°-40°=50°。(注:此处原解析思路有误,正确解法应为∠DOF=∠DOE+∠EOF=40°+90°=130°)
∠DOF=∠DOE+∠EOF=40°+90°=130°。
C
2. 已知$OA\perp OC$,且$\angle AOB与\angle AOC的度数之比为2:3$,则$\angle BOC$的大小是 (
C
)
A.$30^\circ$
B.$150^\circ$
C.$30^\circ或150^\circ$
D.不能确定
答案:C
解析:
∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB与∠AOC的度数之比为2:3,
∴∠AOB=90°×(2/3)=60°,
情况1:OB在∠AOC内部,
∠BOC=∠AOC - ∠AOB=90° - 60°=30°;
情况2:OB在∠AOC外部,
∠BOC=∠AOC + ∠AOB=90° + 60°=150°;
∠BOC的大小是30°或150°,
C
3. 如图,将一副三角板叠放在一起,使直角的顶点重合于点O.
(1) 若$\angle DOC= 30^\circ$,则$\angle AOB= $
150°
.
(2) 若$\angle DOC= 50^\circ$,则$\angle AOB= $
130°
.
(3)$\angle AOB与\angle DOC$有什么数量关系? 为什么?
解:不难发现,∠AOD+∠DOC=90°,∠DOC+∠BOC=90°
∴∠AOB+∠DOC=∠AOD+∠DOC+∠COB+∠DOC
=(∠AOD+∠DOC)+(∠COB+∠DOC)=180°
答案:150°
130°
解:不难发现,∠AOD+∠DOC=90°,∠DOC+∠BOC=90°
∴∠AOB+∠DOC=∠AOD+∠DOC+∠COB+∠DOC
=(∠AOD+∠DOC)+(∠COB+∠DOC)=180°
4. 如图,直线AB,CD相交于点O,已知$\angle AOC= 80^\circ$,射线OE把$\angle BOD$分成两个角,且$\angle BOE与\angle EOD的度数之比为3:5$.
(1) 求$\angle EOB$的大小;
(2) 过点O作射线$OF\perp OE$,求$\angle BOF$的大小.

答案:解:(1)易知,∠BOD=∠AOC=80°
∴$∠EOB=\frac {3}{3+5}∠BOD=30°$
(2)当∠BOF为钝角时,
∠BOF=∠EOB+∠EOF=120°
当∠BOF为锐角时,
∠BOF=∠EOF-∠EOB=60°
综上,∠BOF=60°或120°