19. 早晨,妈妈用热水给小雪加热180g的袋装牛奶。为了使这袋牛奶的温度由12℃升高到42℃,若不计热量损失,则妈妈至少要用60℃的热水多少千克?[水的比热容为$4.2× 10^{3}\ J/(kg·℃)$,该牛奶的比热容为$2.5× 10^{3}\ J/(kg·℃)$]
答案:0.179 kg
解析:
解:牛奶的质量$m_{牛奶}=180\ g=0.18\ kg$,牛奶温度升高$\Delta t_{牛奶}=42^{\circ}C-12^{\circ}C=30^{\circ}C$,热水初温$t_{0水}=60^{\circ}C$,末温$t=42^{\circ}C$,热水温度降低$\Delta t_{水}=60^{\circ}C-42^{\circ}C=18^{\circ}C$。
牛奶吸收的热量$Q_{吸}=c_{牛奶}m_{牛奶}\Delta t_{牛奶}=2.5× 10^{3}\ J/(kg·℃)×0.18\ kg×30^{\circ}C=1.35× 10^{4}\ J$。
不计热量损失,热水放出的热量$Q_{放}=Q_{吸}=1.35× 10^{4}\ J$。
由$Q_{放}=c_{水}m_{水}\Delta t_{水}$得,热水质量$m_{水}=\frac{Q_{放}}{c_{水}\Delta t_{水}}=\frac{1.35× 10^{4}\ J}{4.2× 10^{3}\ J/(kg·℃)×18^{\circ}C}\approx0.179\ kg$。
0.179 kg
20. 小明在与小华探究沙子和水谁的“容热”本领大时,用两个相同的容器分别装有质量都是200g的沙子和水,再用两只完全相同的酒精灯在相同环境下分别对其进行加热。他们绘制出沙子与水的温度随加热时间变化的图像如图所示。已知酒精的热值是$3.0× 10^{7}\ J/kg$,水的比热容是$4.2× 10^{3}\ J/(kg·℃)$,设加热时酒精灯平均1min消耗0.8g酒精,则:
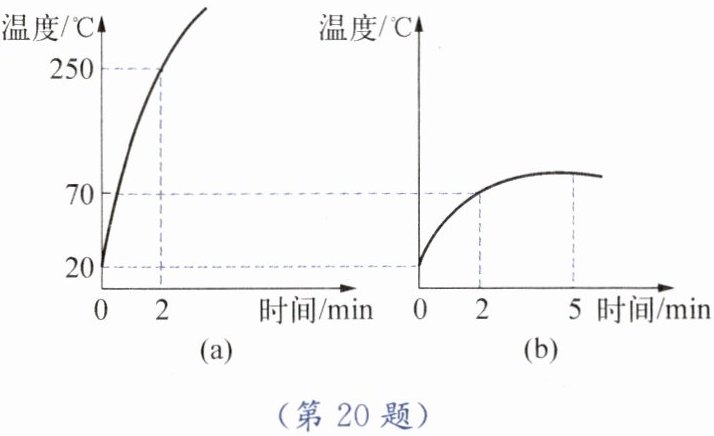
(1)图(a)和图(b)中哪个是沙子吸热升温的图像?为什么?
(2)对水持续加热10min,消耗的酒精若完全燃烧,则会放出多少热量?
(3)试求出沙子的比热容。(不计热量损失)
答案:(1)图(a) 沙子的比热容小于水,相同质量的水和沙子吸收相同的热量,沙子的温度升得高 (2)2.4×10⁵J (3)沙子的比热容为0.91×10³J/(kg·°C)
解析:
(1)图(a)。沙子的比热容小于水,相同质量的水和沙子吸收相同的热量,沙子的温度升得高。
(2)消耗酒精的质量:$m = 0.8\ g/min × 10\ min = 8\ g = 0.008\ kg$,放出的热量:$Q_{放} = mq = 0.008\ kg × 3.0 × 10^{7}\ J/kg = 2.4 × 10^{5}\ J$。
(3)由图(b)可知,水加热10min温度从$20^{\circ}C$升高到$70^{\circ}C$,$\Delta t_{水} = 70^{\circ}C - 20^{\circ}C = 50^{\circ}C$,水吸收的热量:$Q_{水吸} = c_{水}m_{水}\Delta t_{水} = 4.2 × 10^{3}\ J/(kg·^{\circ}C) × 0.2\ kg × 50^{\circ}C = 4.2 × 10^{4}\ J$,则1min水吸收热量:$Q_{1} = \frac{4.2 × 10^{4}\ J}{10} = 4.2 × 10^{3}\ J$。沙子加热2min吸收热量:$Q_{沙吸} = 2Q_{1} = 2 × 4.2 × 10^{3}\ J = 8.4 × 10^{3}\ J$,沙子温度从$20^{\circ}C$升高到$250^{\circ}C$,$\Delta t_{沙} = 250^{\circ}C - 20^{\circ}C = 230^{\circ}C$,沙子比热容:$c_{沙} = \frac{Q_{沙吸}}{m_{沙}\Delta t_{沙}} = \frac{8.4 × 10^{3}\ J}{0.2\ kg × 230^{\circ}C} \approx 0.18 × 10^{3}\ J/(kg·^{\circ}C)$。
1