8. 如图11-2-3所示是某种健身器械,AOB可视为杠杆。小明竖直向下拉杠杆,重物被抬起,此时阻力臂
小于
动力臂。小明想通过增大向下的拉力来加大训练强度,请你根据杠杆平衡条件,给小明提出一条合理的建议:
增加重物质量或握点B向左移(减小动力臂)
。
答案:8.小于 增加重物质量或握点B向左移(减小动力臂)
9. 在高速列车上,乘务员用图11-2-4所示的小推车销售食品。当小推车的前轮碰到障碍物时,他向下按扶把,这时小推车可以视为杠杆,支点是______
后轮
(前轮/后轮);当后轮遇到障碍物时,他向上提扶把,这时小推车可以视为______
省力
(省力/费力/等臂)杠杆。若小推车的总重力为600 N,后轮遇到障碍物时动力臂为阻力臂的3倍,此时乘务员提小推车的力为______
200
N。
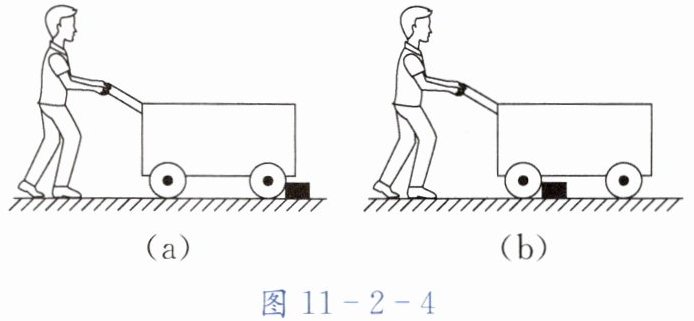
答案:9.后轮 省力 200
10. 如图11-2-5所示,AOB为一机械设备的简化示意图,可以把它看成是一个杠杆(自重不计)。已知AO= 2OB,AOB可绕点O转动,B端挂一重为40 N的物体,要使OB在水平位置保持静止,至少需要在A端施加力F= ______N,并在图上画出力F的方向。

答案:10.20 见图答11−2−1

11. 如图11-2-6所示,独轮车和车内石头的总质量为90 kg,车轴支点为点O,在点A施加竖直向上的力F抬起独轮车。

(1)该独轮车在使用时是省力杠杆还是费力杠杆?
(2)将车把抬起时,作用在车把上的力是多大?(g取10 N/kg)
答案:1. (1)
由图可知,动力臂$L_1 = 1.6m$,阻力臂$L_2=0.4m$。
因为动力臂大于阻力臂($L_1>L_2$),根据杠杆的分类:当$L_1 > L_2$时,$F_1<F_2$,所以该独轮车是省力杠杆。
2. (2)
解:首先计算独轮车和车内石头的总重力$G = mg$,已知$m = 90kg$,$g = 10N/kg$,则$G=mg=90kg×10N/kg = 900N$。
根据杠杆平衡条件$F_1L_1=F_2L_2$(这里$F_1 = F$,$F_2 = G$),可得$F× L_1=G× L_2$。
已知$L_1 = 1.6m$,$L_2 = 0.4m$,$G = 900N$,将其代入$F× L_1=G× L_2$中,$F=\frac{G× L_2}{L_1}$。
把数值代入公式:$F=\frac{900N×0.4m}{1.6m}=225N$。
综上,(1)该独轮车是省力杠杆;(2)作用在车把上的力是$225N$。
12. 如图11-2-7所示,OAB为轻质杠杆,可绕点O自由转动,在B端施加一个动力可使杠杆在水平位置平衡。请在图中按下列三种情况分别画出这个力,并标出对应的力臂。

(a)省力杠杆
(b)费力杠杆
(c)等臂杠杆
答案:12.见图答11−2−2(答案合理即可)
