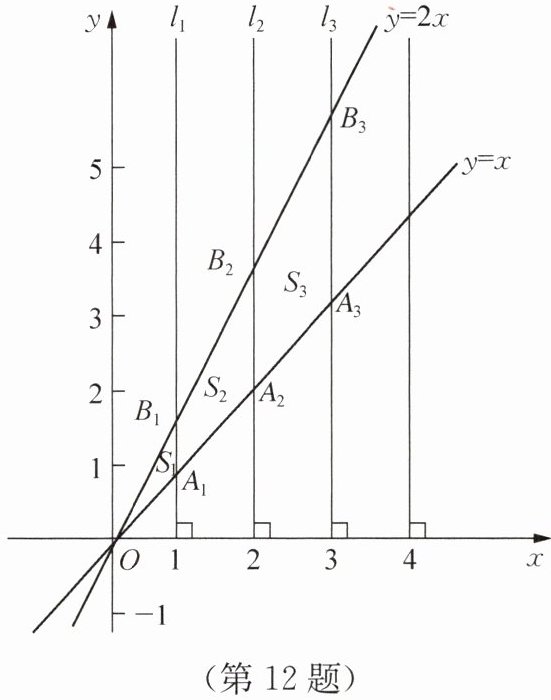
12. 如图,直线$l_1⊥x$轴,垂足为点$(1,0)$,直线$l_2⊥x$轴,垂足为点$(2,0)$,直线$l_3⊥x$轴,垂足为点$(3,0)$,…,直线$l_n⊥x$轴,垂足为点$(n,0)$(其中$n$为正整数).函数$y= x的图象与直线l_1$,$l_2$,$l_3$,…,$l_n分别交于点A_1$,$A_2$,$A_3$,…,$A_n$；函数$y= 2x的图象与直线l_1$,$l_2$,$l_3$,…,$l_n分别交于点B_1$,$B_2$,$B_3$,…,$B_n$,如果$\triangle OA_1B_1的面积记作S_1$,四边形$A_1A_2B_2B_1的面积记作S_2$,四边形$A_2A_3B_3B_2的面积记作S_3$,…,四边形$A_{n-1}A_nB_nB_{n-1}的面积记作S_n$,求$S_{2024}$.