1. 列表梳理正比例函数的图象和性质:
| 函数表达式 | ______ | ______ |
| 函数图象 | | |
| 图象经过的象限 | ______ | ______ |
| 函数变化趋势 | ______ | ______ |
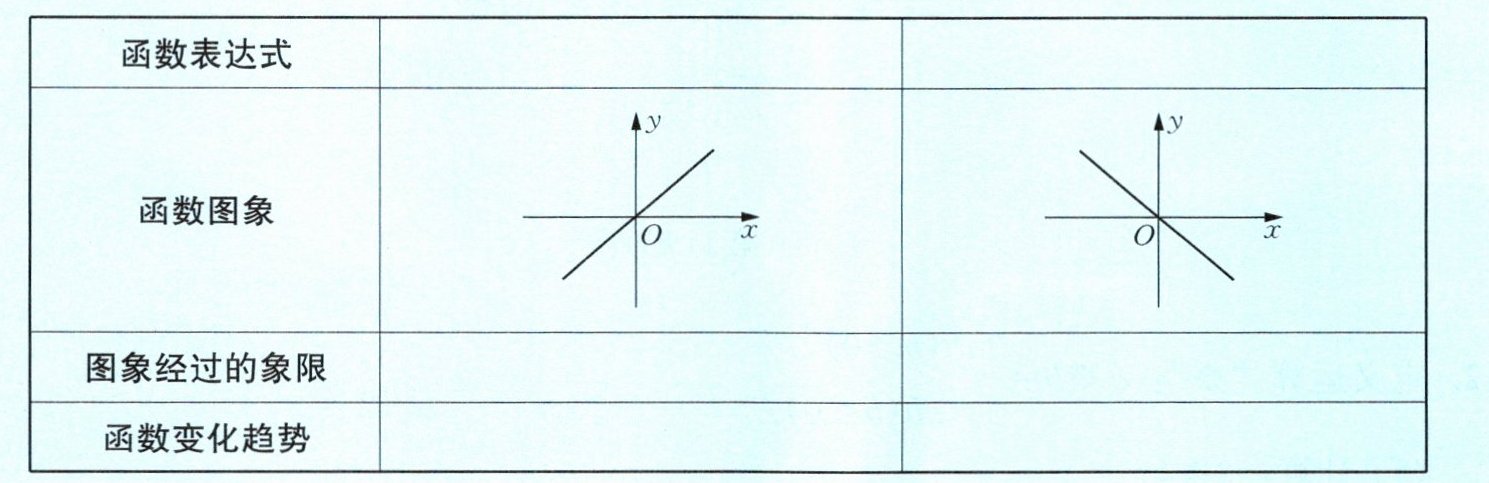
答案:y=kx(k>0),y=kx(k<0),一、三,二、四,y 随x 的增大而增大,y 随x 的增大而减小
解析:
| 函数表达式 | $y=kx(k>0)$ | $y=kx(k<0)$ |
|--------------------|-----------------------|-----------------------|
| 函数图象 | (对应第一列给定的上升直线图) | (对应第二列给定的下降直线图) |
| 图象经过的象限 | 一、三 | 二、四 |
| 函数变化趋势 | $y$ 随 $x$ 的增大而增大 | $y$ 随 $x$ 的增大而减小 |
2. 函数$y= -3x$的图象经过(
B
)
A.第一、三象限
B.第二、四象限
C.第一、二象限
D.第三、四象限
答案:B
解析:
对于函数$y = -3x$,它是正比例函数,其中比例系数$k=-3$。
因为当$k<0$时,正比例函数$y = kx$的图象经过第二、四象限,而$-3<0$,所以函数$y = -3x$的图象经过第二、四象限。
B
3. 已知$A(x_1,y_1)$,$B(x_2,y_2)是关于x的函数y= mx$的图象上的两点,当$x_1<x_2$时,$y_1<y_2$,则$m$的取值范围是(
A
)
A.$m>0$
B.$m<0$
C.$m>1$
D.$m<1$
答案:A
解析:
因为点$A(x_1,y_1)$,$B(x_2,y_2)$在函数$y = mx$的图象上,所以$y_1=mx_1$,$y_2=mx_2$。
已知当$x_1 < x_2$时,$y_1 < y_2$,即$mx_1 < mx_2$,移项可得$m(x_2 - x_1) > 0$。
因为$x_1 < x_2$,所以$x_2 - x_1 > 0$,则$m > 0$。
A
4. 在探究正比例函数$y= kx$($k$为常数,$k≠0$)的图象时,小蒋列表如下,其中$m$的值为
-6
.
| $x$ | ... | 2 | 1 | 0 | -1 | -2 | ... |
| $y$ | ... | 12 | 6 | 0 | $m$ | -12 | ... |

答案:-6
解析:
当$x = 1$时,$y = 6$,代入$y=kx$,得$6=k×1$,解得$k = 6$,所以函数解析式为$y=6x$。当$x=-1$时,$m=6×(-1)=-6$。
$-6$
5. 下列正比例函数中,$y随x$增大而减小的有
②③
,其中,减小最快的是
②
.(填序号)
①$y= 2x$;②$y= -3x$;③$y= (\sqrt{2}-\sqrt{3})x$;④$y= \frac{\sqrt{10}}{2}x$.
答案:②③,②
6. 已知正比例函数$y= 2x$,当$1≤x≤2$时,$y$的最小值为(
C
)
A.4
B.5
C.2
D.0
答案:C
解析:
因为正比例函数$y = 2x$中,$k = 2>0$,所以$y$随$x$的增大而增大。当$1\leq x\leq2$时,$x$取最小值$1$时,$y$有最小值,$y_{min}=2×1 = 2$。
C
7. 如图所示是光从空气进入水中的光路图,以入射点$O$为原点,建立平面直角坐标系,并设$y_1= k_1x$,$y_2= k_2x$.关于$k_1与k_2$的关系,下列选项中正确的是(
D
)

A.$k_2<0<k_1$
B.$k_1<0<k_2$
C.$k_1<k_2<0$
D.$k_2<k_1<0$
答案:D
解析:
由图像可知,$y_1=k_1x$经过第二、四象限,$y_2=k_2x$经过第四象限,所以$k_1<0$,$k_2<0$。
在第四象限取相同的$x$值,对应的$y_1$的值大于$y_2$的值,即$k_1x > k_2x$($x>0$),两边同时除以$x$($x>0$,不等号方向不变),得$k_1 > k_2$。
综上,$k_2 < k_1 < 0$。
D