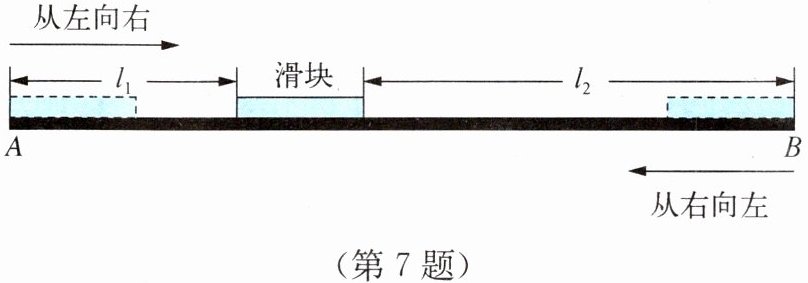
7. 某动力科学研究院的实验室内装有一段笔直的轨道 $ AB $,长度为 1 m 的金属滑块在上面做往返滑动. 如图,滑块首先沿 $ AB $ 方向从左向右匀速滑动,滑动速度为 9 m/s,滑动开始前滑块左端与点 $ A $ 重合,当滑块右端到达点 $ B $ 时,停顿 2 s,然后再以小于 9 m/s 的速度匀速返回,直到左端与点 $ A $ 重合,滑动停止. 设当时间为 $ t \ s $ 时,滑块左端和点 $ A $ 的距离为 $ l_1 \ m $,右端和点 $ B $ 的距离为 $ l_2 \ m $,记 $ d = l_1 - l_2 $,$ d $ 与 $ t $ 具有函数关系,已知滑块在从左向右滑动的过程中,当 $ t = 4.5 $ 和 5.5 时,与之对应的 $ d $ 的两个值互为相反数;滑块从点 $ A $ 出发到最后返回点 $ A $,整个过程总用时 27 s(含停顿时间). 请你根据所给条件解决下列问题:
(1)滑块从点 $ A $ 到点 $ B $ 的滑动过程中,$ d $ 的值
由负到正
(填“由负到正”或“由正到负”);
(2)写出滑块从点 $ B $ 到点 $ A $ 滑动过程中 $ d $ 关于 $ t $ 的函数表达式;
d=-12t+234
(3)在整个往返过程中,求当 $ d = 18 $ 时,$ t $ 的值.
当t=6或18时,d=18
解析:
(1)由负到正
(2)设轨道$AB$的长度为$L$米,滑块从点$A$到点$B$的滑动过程中,$l_1 = 9t$,$l_2 = L - (9t + 1)$,则$d = l_1 - l_2 = 9t - [L - (9t + 1)] = 18t + 1 - L$。因为当$t = 4.5$和$t = 5.5$时,$d$的值互为相反数,所以$18×4.5 + 1 - L + 18×5.5 + 1 - L = 0$,解得$L = 91$。滑块从$A$到$B$用时$\frac{91 - 1}{9} = 10$秒,停顿$2$秒,设返回速度为$v$ m/s,返回用时$\frac{91}{v}$秒,总用时$10 + 2 + \frac{91}{v} = 27$,解得$v = 7$。返回过程中,$t$的范围是$12 \leq t \leq 27$,$l_1 = 91 - 7(t - 12)$,$l_2 = 7(t - 12) - 1$,所以$d = l_1 - l_2 = [91 - 7(t - 12)] - [7(t - 12) - 1] = -14t + 253$
(3)当滑块从左向右滑动时,$d = 18t + 1 - 91 = 18t - 90$,令$18t - 90 = 18$,解得$t = 6$。当滑块从右向左滑动时,$d = -14t + 253$,令$-14t + 253 = 18$,解得$t = \frac{235}{14}$(不符合题意,舍去)。综上,$t = 6$