9. 已知直线AB,CD相交于点O,∠AOF= 90°,OA平分∠EOC.
(1)如图①,若∠AOE= 50°,则∠COF=
40
°,∠BOD=
50
°;
(2)如图②,若∠EOC= ∠COF,则∠AOE=
30
°,与∠AOE互补的角有
∠AOD,∠BOC,∠BOE
.
答案:
(1) 40,50. 提示:因为 OA 平分∠EOC,所以∠AOC=∠AOE=50°;因为∠AOF=90°,所以∠COF=∠AOF-∠AOC=90°-50°=40°. 因为∠BOD 与∠AOC 是对顶角,所以,∠BOD=∠AOC=50°
(2) 30;∠AOD,∠BOC,∠BOE. 提示:因为 OA 平分∠EOC,所以∠AOC=∠AOE,∠EOC=2∠AOC;因为∠EOC=∠COF,所以∠COF=2∠AOC. 因为∠AOF=∠AOC+∠COF=90°,所以 3∠AOC=90°,∠AOC=30°,所以∠AOE=30°
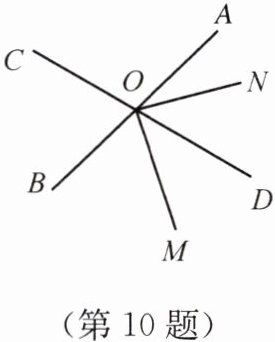
10. 如图,直线AB,CD相交于点O,ON把∠AOD分成两个角,且∠AON与∠NOD的度数之比是2∶3,∠BOC= 75°.
(1)求∠AON的大小.
(2)如果OM平分∠BON,那么OB是∠COM的平分线吗?试说明理由.
答案:
(1) 因为∠AOD 与∠BOC 为对顶角,且∠BOC=75°;所以∠AOD=75°,又因为∠AOD=∠AON+∠NOD,∠AON:∠NOD=2:3,所以∠AON=30°
(2) OB 是∠COM 的角平分线. 因为∠AON=30°,所以∠BON=180°-∠AON=180°-30°=150°. 又因为 OM 平分∠BON,所以∠BOM=$\frac{1}{2}$∠BON=75°. 所以∠BOC=∠BOM,所以 OB 是∠COM 的角平分线
11. 如图,直线EF与MN相交于点O,∠MOE= 30°,将三角板的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部. 操作:将三角板绕点O以3°/s的速度按顺时针方向旋转一周,设运动时间为t s.
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?
(2)若在三角板转动的同时,直线EF也以9°/s的速度绕点O按顺时针方向旋转一周,当一方先旋转完一周时,另一方同时停止转动.
①当t为何值时,EF平分∠AOB?
②EF能否平分∠NOB?若能,请直接写出t的值;若不能,请说明理由.

答案:
(1) 当直角边 OB 恰好平分∠NOE 时,∠NOB=$\frac{1}{2}$∠NOE=$\frac{1}{2}$(180°-30°)=75°,所以 90°-3°·t=75°,解得 t=5. 此时∠MOA=3°×5=15°=$\frac{1}{2}$∠MOE,所以此时 OA 平分∠MOE
(2) ① OE 平分∠AOB,依题意有 30+9t-3t=90÷2,解得 t=2.5;OF 平分∠AOB,依题意有 30+9t-3t=180+90÷2,解得 t=32.5. 综上所述,当 t 为 2.5 或 32.5 时,EF 平分∠AOB ② OB 在 MN 上面,依题意有 180-30-9t=(90-3t)÷2,解得 t=14;OB 在 MN 下面,依题意有 9t-(360-30)=(3t-90)÷2,解得 t=38(舍去). 综上所述,EF 能平分∠NOB,t 为 14