2025年同步练习江苏七年级数学上册苏科版第95页解析答案

10. 如图,已知$\angle 1,$$\angle 2,$$\angle 1＜\angle 2,$用直尺和圆规作两个角,使其大小分别是$\angle 2-\angle 1,$$\angle 1+\angle 2.($不写作法,保留作图痕迹)

答案：
如图,∠AOC=∠2−∠1,∠DOF=∠1+∠2 　　　　　　　

　　　　　　　　　　　　　　　　　　(第10题)

11. 如图,直线AB,CD相交于点O,OE平分$\angle BOD,$$\angle EOF= 90°,$OF平分$\angle BOC$吗？为什么？

答案：平分.因为OE平分∠BOD,所以∠BOE=∠DOE,因为∠EOF=90°,所以∠BOE+∠BOF=90°,∠DOE+∠COF=180°−∠EOF=90°,因为∠BOE=∠DOE,所以∠BOF=∠COF

解析：

OF平分∠BOC。
因为OE平分∠BOD，所以∠BOE=∠DOE。
因为∠EOF=90°，所以∠BOE+∠BOF=90°。
因为∠COD是平角，所以∠COF+∠DOE+∠EOF=180°，即∠COF+∠DOE+90°=180°，所以∠COF+∠DOE=90°。
因为∠BOE=∠DOE，所以∠BOF=∠COF，即OF平分∠BOC。

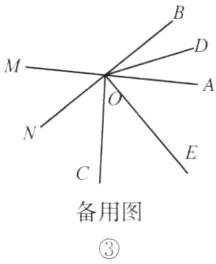
12. (1)如图①,OC是$\angle AOB$内的一条射线,OD,OE分别平分$\angle AOB,$$\angle AOC. 若\angle BOC= 90°,求\angle DOE.(2)$小明在完成以上问题解答后,作如下变式探究：
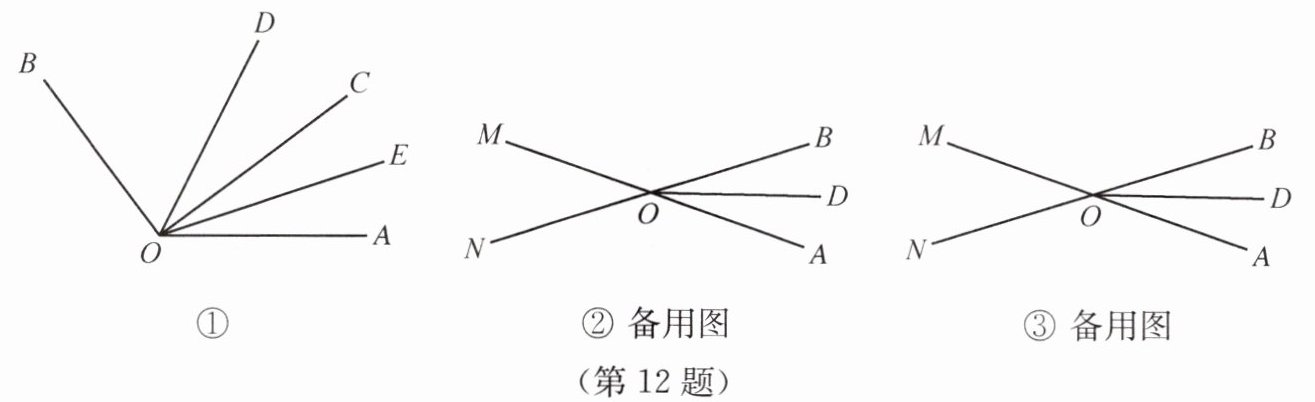
如图①,若$\angle BOC= m°,则\angle DOE= ______.(3)$已知直线AM,BN相交于点O,若OC是$\angle AOB$外一条射线,且不与OM,ON重合,OD,OE分别平分$\angle AOB,$$\angle AOC,当\angle BOC= m°$时,求$\angle DOE.($在备用图中画出示意图求解)

答案：

(1)∠DOE=45°.设∠AOC=α°,则∠AOB=∠AOC+∠BOC=α°+90°,因为OD平分∠AOB,OE平分∠AOC,所以∠DOE =∠AOD−∠AOE=$\frac{1}{2}$∠AOB−$\frac{1}{2}$∠AOC=$\frac{1}{2}$(α°+90°)−$\frac{1}{2}$α°=$\frac{1}{2}$×90°=45°；
(2)$\frac{m°}{2}$.设∠AOC=α°,则∠AOB=∠AOC+∠BOC=α°+m°,因为OD平分∠AOB,OE平分∠AOC,所以∠DOE=∠AOD−∠AOE =$\frac{1}{2}$∠AOB−$\frac{1}{2}$∠AOC=$\frac{1}{2}$(α°+m°)−$\frac{1}{2}$α°=$\frac{m°}{2}$；
(3)①当OC在AM上,即OC在∠BOM之间,设∠AOC=α°,则∠AOB=∠AOC−∠BOC=α°−m°,因为OD平分∠AOB,OE平分∠AOC,所以∠DOE=∠AOD−∠AOE=$\frac{1}{2}$∠AOC−$\frac{1}{2}$∠AOB=$\frac{1}{2}$α°−$\frac{1}{2}$(α°−m°)=$\frac{m°}{2}$;②当OC在直线AM下方,且OC在∠MON之间时,∠BOC=∠AOC=m°,∠DOE=∠AOE−∠AOD=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠AOB=$\frac{1}{2}$∠BOC=180°−$\frac{m°}{2}$;③当OC在直线AM下方,且OC在∠AON之间时,由②得,∠BOC=m°,∠DOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠AOB=$\frac{1}{2}$∠BOC=$\frac{m°}{2}$.综上所述,∠DOE=$\frac{m°}{2}$或180°−$\frac{m°}{2}$ 　　　　