9. 如图,两个三角板的直角顶点重合,$\angle BOD= 39^\circ,求\angle AOC$的大小.
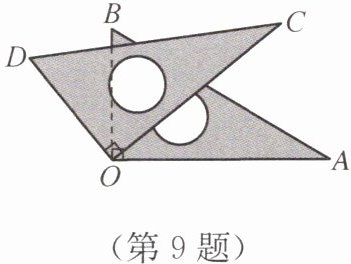
答案:因为∠BOD+∠COB=90°,∠AOC+∠COB=90°,所以∠BOD=∠AOC,因为∠BOD=39°,所以∠AOC=39°
10. 一个角的余角比它的补角的$\frac{2}{3}还少50^\circ,$求这个角的度数.
答案:设这个角为x,则余角为90°-x,补角为180°-x,由题意,得90°-x=$\frac{2}{3}$(180°-x)-50°,解得x=60°.这个角是60°
解析:
设这个角为$x$,则余角为$90^\circ - x$,补角为$180^\circ - x$。由题意,得$90^\circ - x = \frac{2}{3}(180^\circ - x) - 50^\circ$,解得$x = 60^\circ$。这个角是$60^\circ$。
11. (1)如图①,将一副三角板的直角顶点C叠放在一起,$\angle ACB= \angle DCH= 90^\circ.① 若\angle BCH= 35^\circ,则\angle ACD= $
145
$^\circ$;若$\angle ACD= 131^\circ,则\angle BCH= $
49
$^\circ.② 猜想\angle ACD与\angle BCH$之间的数量关系,并说明理由.
(2)如图②,将两个相同的三角板$60^\circ$角的顶点A重合在一起,$\angle ACB= \angle AEF= 90^\circ,直接写出\angle CAF与\angle EAB$之间的数量关系.
$\angle CAF+\angle EAB=120^\circ$

答案:(1)① 145°;49° ② 互补.因为∠BCH=∠DCH+∠BCA-∠ACD=90°+90°-∠ACD=180°-∠ACD,所以∠BCH+∠ACD=180° (2)∠CAF+∠EAB=120°
解析:
(1)① 145;49
② 互补。因为$\angle BCH = \angle DCH + \angle BCA - \angle ACD = 90^\circ + 90^\circ - \angle ACD = 180^\circ - \angle ACD$,所以$\angle BCH + \angle ACD = 180^\circ$
(2)$\angle CAF + \angle EAB = 120^\circ$