8. 数学老师布置了一道思考题:“计算:$(-\frac{1}{12})÷(\frac{1}{3}-\frac{5}{6})$”。小明仔细思考了一番,用了一种特别的方法解决了这个问题:
原式的倒数为$(\frac{1}{3}-\frac{5}{6})÷(-\frac{1}{12})= (\frac{1}{3}-\frac{5}{6})×(-12)= -4+10= 6$,
所以$(-\frac{1}{12})÷(\frac{1}{3}-\frac{5}{6})= \frac{1}{6}$。
请你运用小明的方法计算:$(-\frac{1}{42})÷(\frac{1}{6}-\frac{2}{7}+\frac{2}{3}-\frac{3}{14})$。
答案:$-\frac{1}{14}$
解析:
原式的倒数为$(\frac{1}{6}-\frac{2}{7}+\frac{2}{3}-\frac{3}{14})÷(-\frac{1}{42})$
$=(\frac{1}{6}-\frac{2}{7}+\frac{2}{3}-\frac{3}{14})×(-42)$
$=\frac{1}{6}×(-42)-\frac{2}{7}×(-42)+\frac{2}{3}×(-42)-\frac{3}{14}×(-42)$
$=-7 + 12 - 28 + 9$
$=-14$
所以$(-\frac{1}{42})÷(\frac{1}{6}-\frac{2}{7}+\frac{2}{3}-\frac{3}{14})=-\frac{1}{14}$
9. 已知$a$,$b$,$c$是有理数,$|a|= 4$,$|b|= 9$,$|c|= 6$,且$ab<0$,$bc>0$。求$ab-bc+abc$的值。
答案:126或-306
解析:
因为$|a| = 4$,所以$a = \pm 4$;因为$|b| = 9$,所以$b = \pm 9$;因为$|c| = 6$,所以$c = \pm 6$。
由于$ab < 0$,所以$a$,$b$异号;又因为$bc > 0$,所以$b$,$c$同号。
情况一:当$b = 9$时,$c = 6$,$a = - 4$。
$ab - bc + abc=(-4)×9 - 9×6+(-4)×9×6=-36 - 54 - 216=-306$
情况二:当$b=-9$时,$c = - 6$,$a = 4$。
$ab - bc + abc=4×(-9)-(-9)×(-6)+4×(-9)×(-6)=-36 - 54 + 216=126$
综上,$ab - bc + abc$的值为$126$或$-306$。
10. 将下列各组数进行混合运算(每个数只能用一次),使得运算结果为24。
(1)4,6,8,9;
(2)12,-12,3,-1;
(3)1,-2,2,3。
答案:答案不唯一,如
(1) $8÷4×9+6$
(2) $3×(-12)×(-1)-12$
(3) $[3-(-2)]^{2}-1$
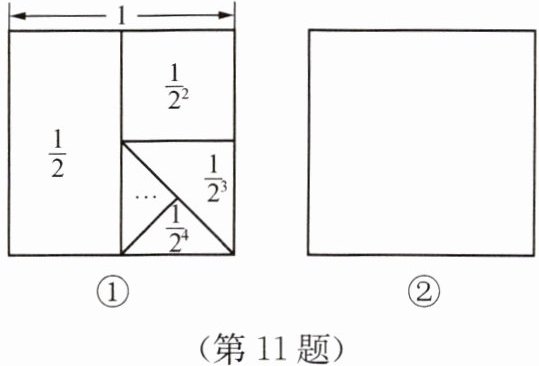
11. 在数学活动中,小明在边长为1的正方形中设计了如图①所示的图形。
(1)根据这个图形,可以直接写出$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{2^n}=$
$1-\frac{1}{2^{n}}$
;
(2)请你在图②中再设计一个能表示$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{2^n}$的图形。
答案不唯一.只要保证每次划分后的区域面积是上次的一半即可,可以划分为两个三角形,也可以划分为两个长方形,等等
答案:
(1) $1-\frac{1}{2^{n}}$.该式子可以看作大正方形去除最后一块三角形的区域面积之和,大正方形面积为1,最后一块三角形的面积为$\frac{1}{2^{n}}$
(2) 答案不唯一.只要保证每次划分后的区域面积是上次的一半即可,可以划分为两个三角形,也可以划分为两个长方形,等等