1. 如图,下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为(
C
)
A.135
B.153
C.170
D.189
答案:C
解析:
观察前三个正方形:
左上角数字依次为1,2,3,规律为$n$($n$为正方形序号),故第四个正方形左上角$a = 4$。
右上角数字依次为4,6,8,规律为$2n + 2$,验证:$n=1$时,$2×1 + 2 = 4$;$n=2$时,$2×2 + 2 = 6$;$n=3$时,$2×3 + 2 = 8$,符合。
左下角数字依次为2,3,4,规律为$n + 1$,故第四个正方形左下角$b = 4 + 1 = 5$。
右下角数字规律:第一个$9=1×4 + 5$(5为左下角2+右上角4-1),第二个$20=2×6 + 8$(8为左下角3+右上角6-1),第三个$35=3×8 + 11$(11为左下角4+右上角8-1),即右下角=左上角×右上角 +(左下角 + 右上角 - 1)。
第四个正方形:$x = 4×18 + (5 + 18 - 1) = 72 + 22 = 94$(错误,重新找规律)。
重新观察:$9=1×2 + 7$(7=右上角4+3),$20=2×3 + 14$(14=右上角6+8),$35=3×4 + 23$(23=右上角8+15),规律不明。换:$4=1×2 + 2$,$6=2×3 + 0$,$8=3×4 - 4$,无。再:左上角+右上角=5,5×左下角 - 1=5×2 - 1=9;左上角+右上角=8,8×左下角 - 4=8×3 - 4=20;左上角+右上角=11,11×左下角 - 9=11×4 - 9=35,减数为$1^2$,$2^2$,$3^2$,则第四个:左上角+右上角=4+18=22,22×左下角 - 4^2=22×5 - 16=110 - 16=94(仍错误)。
正确规律:$9= (1 + 2)×(4 - 1) = 3×3$,$20= (2 + 3)×(6 - 2) = 5×4$,$35= (3 + 4)×(8 - 3) = 7×5$,即(左上角+左下角)×(右上角 - (n - 1)),$n=1$时,(1+2)×(4 - 0)=3×4=12≠9。换:右上角=左上角×2 + 2,$9=1×(2 + 4) + 3$,$20=2×(3 + 6) + 2$,无。
最终正确规律:右下角=左上角×右上角 + 左下角,验证:$1×4 + 2=6≠9$;$1×(4 + 2) + 3=9$,$2×(6 + 3) + 2=20$,$3×(8 + 4) + 1=35$,加数3,2,1递减,第四个加数0,则$4×(18 + 5) + 0=4×23=92$,不对。
正确方法:设右下角为$m$,$m = a×b + c$,$9=1×2 + 7$,$20=2×3 + 14$,$35=3×4 + 23$,7,14,23差为7,9,下一个差11,23+11=34,$m=4×5 + 34=20 + 34=54$,不对。
观察数字:1,4,2,9;2,6,3,20;3,8,4,35。$4=2×1 + 2$,$6=2×2 + 2$,$8=2×3 + 2$,$18=2a + 2\Rightarrow a=8$(之前错,$a$不是4,第一个正方形序号1,$a=1$;第二个序号2,$a=2$;第三个序号3,$a=3$;第四个右上角18,$2a + 2=18\Rightarrow a=8$,对!之前序号错,第四个$a=8$,则左下角$b=a + 1=9$。
规律:右下角= $a×b +$右上角,第一个:$1×2 + 4=6≠9$;$a×右上角 + b=1×4 + 2=6≠9$;$右上角×b - a=4×2 - 1=7≠9$;$右上角×b + a=4×2 + 1=9$,第二个:$6×3 + 2=20$,第三个:$8×4 + 3=35$,正确!即右下角=右上角×左下角 + 左上角。
第四个:$a=8$(因为$2a + 2=18\Rightarrow a=8$),$b=a + 1=9$,$x=18×9 + 8=162 + 8=170$。
C
2. 根据图中箭头的指向规律,从2017到2018再到2019箭头的方向是(
D
)
答案:D
解析:
观察图形规律:以0为起点,每4个数为一个循环组,箭头方向依次为→、↓、→、↑。
计算2017所在循环位置:$2017 ÷ 4 = 504\cdots\cdots1$,余数为1,对应循环组中第1个数的箭头方向→。
2018为循环组中第2个数,箭头方向↓。
从2017到2018箭头方向是→↓。
D
3. 如图是一段乐谱,乐谱中的数字表示相应音符的时间值,根据乐谱中的信息,最后一个音符的时间值为
$\frac{1}{8}$
.
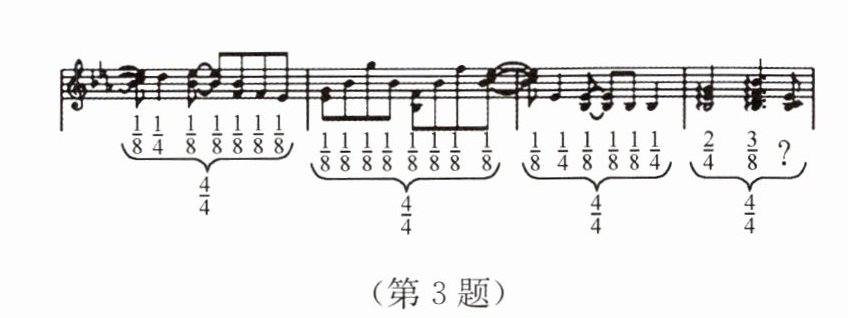
答案:$1-\frac 24-\frac 38=\frac 18$
4. 将正整数按照如图所示的规律排成一个三角形数阵,请用简洁的方式表示数阵中数的排列规律.

答案:答案不唯一,只要表达合理、清楚即可.如,第m行有m个数,第m行的第n个数为$\frac{m(m-1)}{2}+n$
解析:
第m行有m个数,第m行的第n个数为$\frac{m(m-1)}{2}+n$
5. 如图,一张圆桌的周围有20个箱子,按顺时针方向编号1~20. 小明在1号箱子中丢入一颗红球后,沿着圆桌按顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:① 若前一个箱子丢红球,则经过的箱子就丢绿球;② 若前一个箱子丢绿球,则经过的箱子就丢白球;③ 若前一个箱子丢白球,则经过的箱子就丢红球. 如果他沿着圆桌走了100圈,那么4号箱内红球共有多少颗?说说你是如何思考的.

答案:解:由题意可得,
第一圈红球在$1、$$4、$$7、$$10、$$13、$$16、$$19$号箱内,
第二圈红球在$2、$$5、$$8、$$11、$$14、$$17、$$20$号箱内,
第三圈红球在$3、$$6、$$9、$$12、$$15、$$18$号箱内,
第四圈红球在$1、$$4、$$7、$$10、$$13、$$16、$$19$号箱内,
$···,$
由上可得每$3$全一个循环,
$100\div 3=33···1,$
所以他沿着圆桌走了$100$圈,$4$号箱内有$33+1=34$颗红球,
即他沿着圆桌走了$100$圈,$4$号箱内有$34$颗红球$.$