8. 平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①,一束光线m射到平面镜a上,被a反射后的光线为n,则∠1= ∠2.如图②,一束光AB先后经平面镜OM,ON反射后,反射光线CD与AB平行.若∠ABM= 25°,则∠DCN的大小为______
65°
.
答案:65°
解析:
∵∠ABM=25°,∠ABM=∠OBC,
∴∠OBC=25°,
∴∠ABC=180°-∠ABM-∠OBC=130°,
∵AB//CD,
∴∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=50°,
∵∠DCN=∠OCB,∠OCB+∠BCD+∠DCN=180°,
∴∠DCN=(180°-∠BCD)÷2=65°
65°
9. 如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.若∠ABE= 138°,∠CDF= 162°,则∠EPF的大小为______
60°
.
答案:60°
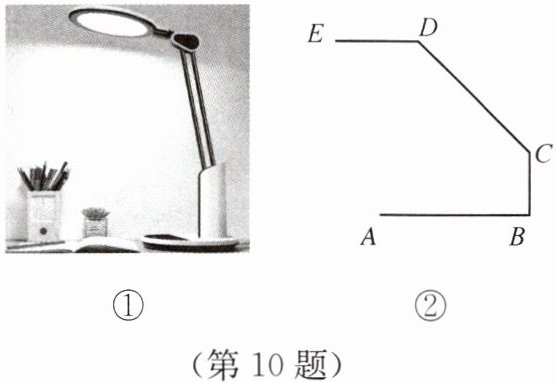
10. 为了保护眼睛,小明将台灯更换为护眼台灯(图①),其侧面示意图(台灯底座高度忽略不计)如图②所示,其中BC⊥AB,ED//AB.经使用发现,当∠DCB= 140°时,台灯光线最佳,此时∠EDC的大小为______
130°
.
答案:130°
解析:
过点C作CF//AB,
∵ED//AB,
∴ED//CF,
∵BC⊥AB,
∴∠ABC=90°,
∵CF//AB,
∴∠BCF=∠ABC=90°,
∵∠DCB=140°,
∴∠DCF=∠DCB - ∠BCF=140° - 90°=50°,
∵ED//CF,
∴∠EDC + ∠DCF=180°,
∴∠EDC=180° - ∠DCF=180° - 50°=130°。
130°
11. 如图,点N在线段CD上,ED与FN交于点M,∠C= ∠1,∠2= ∠3.
(1)判断AB与CD是否平行,并说明理由;
(2)若∠D= 40°,∠EMF= 80°,求∠AEP的大小.

答案:
(1) 平行. 因为∠2=∠3,所以CE//AF,因为CE//AF,所以∠C=∠FND,又因为∠C=∠1,所以∠FND=∠1,所以AB//CD
(2) 因为∠D=40°,AB//CD,∠EMF=80°,所以∠BED=40°,∠2=∠3=80°,所以∠BEC=80°+40°=120°,所以∠AEP=∠BEC=120°