1 计算下面各组合图形的面积。(单位:cm)
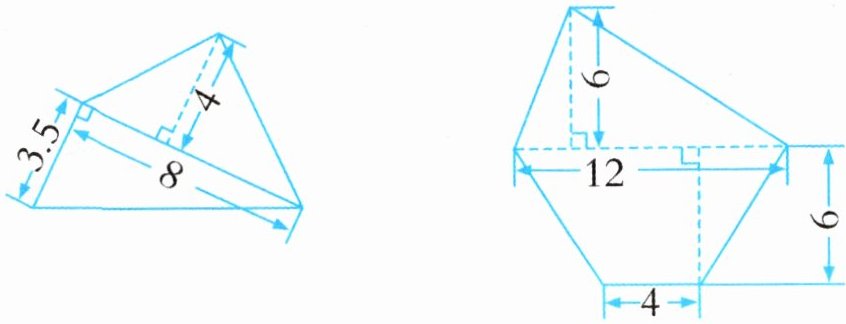
答案:1. 对于第一个组合图形:
这个组合图形由两个三角形组成,根据三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为高)。
第一个三角形:底$a_1 = 8\mathrm{cm}$,高$h_1 = 3.5\mathrm{cm}$,其面积$S_1=\frac{1}{2}×8×3.5$;第二个三角形:底$a_2 = 8\mathrm{cm}$,高$h_2 = 4\mathrm{cm}$,其面积$S_2=\frac{1}{2}×8×4$。
组合图形面积$S = S_1 + S_2$。
$S=\frac{1}{2}×8×3.5+\frac{1}{2}×8×4$
根据乘法分配律$ac + bc=(a + b)c$,这里$c = \frac{1}{2}×8$,$a = 3.5$,$b = 4$。
$S=\frac{1}{2}×8×(3.5 + 4)$
先计算括号内$3.5+4 = 7.5$,再计算$\frac{1}{2}×8×7.5$。
$\frac{1}{2}×8 = 4$,则$S = 4×7.5=30(\mathrm{cm}^2)$。
2. 对于第二个组合图形:
这个组合图形由一个三角形和一个梯形组成。
三角形面积公式$S_{\triangle}=\frac{1}{2}ah$($a = 12\mathrm{cm}$,$h = 6\mathrm{cm}$),梯形面积公式$S_{ 梯}=\frac{(a + b)h}{2}$($a = 4\mathrm{cm}$,$b = 12\mathrm{cm}$,$h = 6\mathrm{cm}$)。
$S_{\triangle}=\frac{1}{2}×12×6$,$S_{ 梯}=\frac{(4 + 12)×6}{2}$。
$S_{\triangle}=36\mathrm{cm}^2$,$S_{ 梯}=\frac{16×6}{2}=48\mathrm{cm}^2$。
组合图形面积$S=S_{\triangle}+S_{ 梯}$。
$S = 36+48=84(\mathrm{cm}^2)$。
综上,第一个组合图形面积是$30\mathrm{cm}^2$,第二个组合图形面积是$84\mathrm{cm}^2$。
2 解决问题。
(1)下图所示的花坛里有三种花,牡丹、月季和玫瑰各占地多少平方米?这个花坛共有多少平方米?

(2)下图是一个排水沟的横截面图,求涂色部分的面积。(单位:dm)

(3)一个指示牌的形状是如图所示的组合图形,求它的面积。

(4)沙漏是古代的一种计时工具。你能计算出下面的沙漏剪影的面积吗?(单位:cm)

答案:(1) 牡丹:3.8×4÷2=7.6(m²);月季:4.2×4=16.8(m²);玫瑰:(5+1.2)×4÷2=12.4(m²);花坛总面积:7.6+16.8+12.4=36.8(m²)。
(2) 长方形面积:9×4=36(dm²);空白梯形面积:(1.6+3.2)×2.4÷2=5.76(dm²);涂色面积:36-5.76=30.24(dm²)。
(3) 长方形面积:20×10=200(cm²);三角形面积:20×10÷2=100(cm²);指示牌面积:200+100=300(cm²)。
(4) 梯形高:(3.5-0.5)÷2=1.5(cm);一个梯形面积:(3+0.4)×1.5÷2=2.55(cm²);两个梯形面积:2.55×2=5.1(cm²);中间长方形面积:0.4×0.5=0.2(cm²);沙漏面积:5.1+0.2=5.3(cm²)。
解析:
由于缺少题目中的插图信息,无法进行具体的计算和作答。请提供插图中的关键数据(如图形的边长、半径、高、底等),以便完成各题的解答。