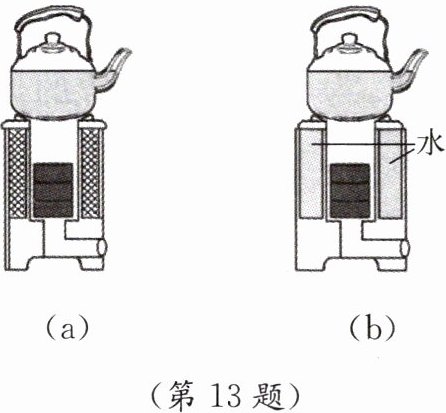
13. 如图(a)所示,在一个标准大气压下,普通煤炉把壶内20°C、5 kg的水烧开需完全燃烧一定质量的煤,此过程中,烧水效率为28%。为提高煤炉效率,科研人员设计了双加热煤炉,如图(b)所示,在消耗等量煤烧开壶内初温相同、等量水的过程中,还可额外把炉壁间的10 kg水从20°C加热至40°C。已知q煤$= 3×10^7J/kg、$c水$= 4.2×10^3J/(kg·°C),$在上述过程中,求:
(1)普通煤炉完全燃烧煤的质量。
(2)双加热煤炉的烧水效率。
答案:解:
(1)在一个标准大气压下,水的沸点为100°C,普通煤炉中水吸收的热量:
Q_{\text{吸}} = c_{\text{水}}m_{\text{水}}\Delta t = 4.2×10^{3}\,\text{J/(kg·°C)}×5\,\text{kg}×(100°C - 20°C) = 1.68×10^{6}\,\text{J}
由$\eta=\frac{Q_{\text{吸}}}{Q_{\text{放}}}$得,煤完全燃烧放出的热量:
$Q_{\text{放}}=\frac{Q_{\text{吸}}}{\eta}=\frac{1.68×10^{6}\,\text{J}}{28\%}=6×10^{6}\,\text{J}$
由$Q_{\text{放}}=mq$得,普通煤炉完全燃烧煤的质量:
$m_{\text{煤}}=\frac{Q_{\text{放}}}{q_{\text{煤}}}=\frac{6×10^{6}\,\text{J}}{3×10^{7}\,\text{J/kg}}=0.2\,\text{kg}$
(2)双加热煤炉额外加热10kg水吸收的热量:
$Q_{\text{吸}}' = c_{\text{水}}m_{\text{水}}'\Delta t' = 4.2×10^{3}J/(kg·℃)×10\,\text{kg}×(40°C - 20°C)=8.4×10^{5}\,\text{J}$
双加热煤炉中水吸收的总热量:
$Q_{\text{吸总}}=Q_{\text{吸}} + Q_{\text{吸}}'=1.68×10^{6}\,\text{J}+8.4×10^{5}\,\text{J}=2.52×10^{6}\,\text{J}$
双加热煤炉消耗煤的质量与普通煤炉相同,故$Q_{\text{放}}=6×10^{6}\,\text{J}$,则双加热煤炉的烧水效率:
$\eta'=\frac{Q_{\text{吸总}}}{Q_{\text{放}}}×100\%=\frac{2.52×10^{6}\,\text{J}}{6×10^{6}\,\text{J}}×100\% = 42\%$
答:
(1)普通煤炉完全燃烧煤的质量为0.2kg;
(2)双加热煤炉的烧水效率为42%。