7. 已知水的比热容为$4.2×10^3 J/(kg·℃),$则2 kg水温度升高1 ℃需要吸收的热量为
$8.4×10^{3}$
J。已知煤油的比热容为水的1/2,则2 kg煤油温度升高1 ℃需要吸收的热量为
$4.2×10^{3}$
J。
答案:解:水吸收的热量:$Q_{水吸}=c_{水}m_{水}\Delta t=4.2×10^{3}J/(kg·℃)×2\ \text{kg}×1\ \text{℃}=8.4×10^{3}\ \text{J} $
煤油的比热容:$c_{煤油}=\frac{1}{2}c_{水}=\frac{1}{2}×4.2×10^{3}J/(kg·℃)=2.1×10^{3}J/(kg·℃) $
煤油吸收的热量:$Q_{煤油吸}=c_{煤油}m_{煤油}\Delta t=2.1×10^{3}J/(kg·℃)×2\ \text{kg}×1\ \text{℃}=4.2×10^{3}\ \text{J} $
$8.4×10^{3};$$4.2×10^{3} $
8. 在完全隔热的装置内,用同一热源分别给100 g水和100 g某种油加热,其温度随时间变化的关系如图所示。已知水的比热容为$4.2×10^3 J/(kg·℃),$试问:
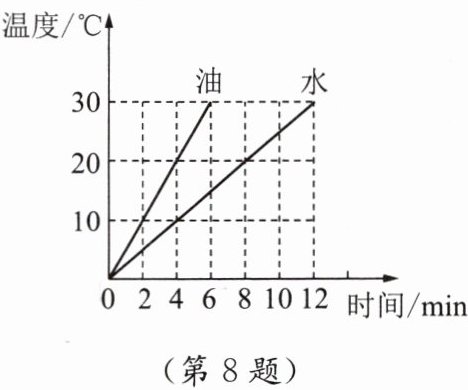
(1)100 g水和100 g这种油每分钟分别吸收多少热量?
(2)这种油的比热容是多大?
答案:解:(1)由图可知,100g水加热12分钟,温度从0℃升高到30℃,水的质量$m_{水}=100g=0.1kg$,温度变化$\Delta t_{水}=30℃ - 0℃=30℃$。
水吸收的总热量$Q_{水总}=c_{水}m_{水}\Delta t_{水}=4.2×10^{3}J/(kg·℃)×0.1kg×30℃=1.26×10^{4}J$。
水每分钟吸收的热量$Q_{水每分钟}=\frac{Q_{水总}}{t_{水}}=\frac{1.26×10^{4}J}{12min}=1050J/min$。
因为用同一热源加热,所以油每分钟吸收的热量与水每分钟吸收的热量相同,即$Q_{油每分钟}=Q_{水每分钟}=1050J/min$。
(2)由图可知,100g油加热6分钟,温度从0℃升高到30℃,油的质量$m_{油}=100g=0.1kg$,温度变化$\Delta t_{油}=30℃ - 0℃=30℃$。
油吸收的总热量$Q_{油总}=Q_{油每分钟}×t_{油}=1050J/min×6min=6300J$。
由$Q=cm\Delta t$得,油的比热容$c_{油}=\frac{Q_{油总}}{m_{油}\Delta t_{油}}=\frac{6300J}{0.1kg×30℃}=2.1×10^{3}J/(kg·℃)$。
(1)100g水每分钟吸收1050J热量,100g这种油每分钟吸收1050J热量;(2)这种油的比热容是$2.1×10^{3}J/(kg·℃)$。