例1 计算$7^{2}-6^{2}$的值。
我的思考 可以直接根据平方数的定义来求解,$7^{2}-6^{2}= 7×7-6×6= 49-36= 13$。还可以利用数形结合来求解,如图,先画一个$7×7$的正方形方格图(每个小方格表示$1×1$),然后在这个正方形方格图中用铅笔涂出一个$6×6$的正方形,发现没有涂色的小方格有13个。

我的解答
我的发现 我发现相邻两个自然数的平方数的差就等于把这两个数( )。
活学活用 利用画图的方式求出$9^{2}-8^{2}$的值。

例2 探究$8^{2}-6^{2}$、$7^{2}-3^{2}$的值的规律。
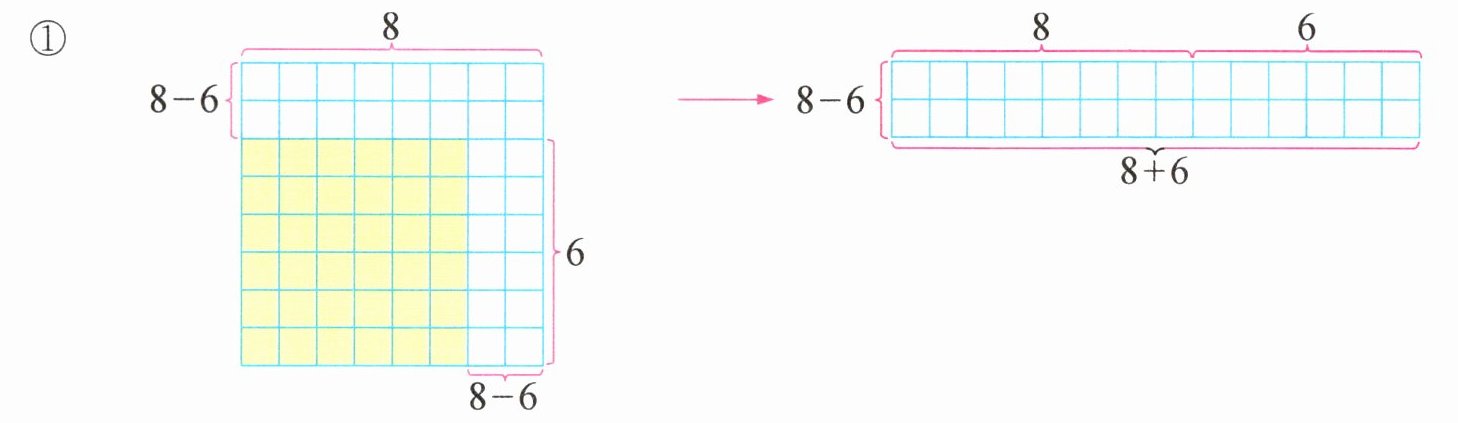
我的思考 利用方格图画图探究。如图①,$8×8的正方形比6×6$的正方形多2行2列,将右下角的2列小方格剪切后可以和上面的2行小方格拼成长方形,这个长方形每行有$(8+6)$个小方格,共有$(8-6)$行。因此,$8^{2}-6^{2}= (8+6)×(8-6)= 28$。
①

同理,图②中$7×7的正方形比3×3$的正方形多4行4列,将右下角的4列小方格剪切后可以和上面的4行小方格拼成长方形,这个长方形每行有$(7+3)$个小方格,共有$(7-3)$行。因此,$7^{2}-3^{2}= (7+3)×(7-3)= 40$。
②

我的解答
我的发现 我发现两个自然数的平方数的差等于这两个数的( )乘这两个数的( )。