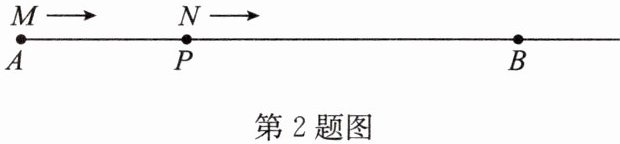
2. 如图,线段 $AB = 32cm$,P 为线段 AB 上一点(不与点 A,B 重合),M,N 两点分别从点 A,P 同时出发沿射线 AB 向右运动,点 M 的运动速度为 $4cm/s$,点 N 的运动速度为 $3cm/s$,设运动时间为 $ts(t ≠ 8)$.
(1) 若 $AP = 8cm$,
① 当 $t = 1$ 时,MN 的长为
$7 \, \text{cm}$
;
② 点 M,N 在运动过程中,线段 BM,MN 之间是否存在某种确定的数量关系?判断并说明理由.
解: $ BM = 4MN $. 理由如下:
因为 $ AP = 8 \, \text{cm} $,$ AB = 32 \, \text{cm} $,所以 $ BP = 24 \, \text{cm} $.
当 $ t = 8 $ 时,点 $ M $,$ N $ 同时到达点 $ B $.
当 $ 0 < t \leq 2 $ 时,$ AM = 4t \, \text{cm} $,$ PN = 3t \, \text{cm} $,$ MP = (8 - 4t) \, \text{cm} $,
所以 $ MN = MP + NP = 8 - 4t + 3t = (8 - t) \, \text{cm} $.
因为 $ BM = 32 - 4t = 4(8 - t) \, \text{cm} $,
所以 $ BM = 4MN $.
当 $ 2 < t < 8 $ 时,$ AM = 4t \, \text{cm} $,$ PN = 3t \, \text{cm} $,$ MP = (4t - 8) \, \text{cm} $.
所以 $ MN = PN - PM = 3t - (4t - 8) = (8 - t) \, \text{cm} $.
因为 $ BM = 32 - 4t = 4(8 - t) \, \text{cm} $,
所以 $ BM = 4MN $.
当 $ t > 8 $ 时,$ AM = 4t \, \text{cm} $,$ PN = 3t \, \text{cm} $,$ AN = (8 + 3t) \, \text{cm} $,
所以 $ MN = AM - AN = 4t - 8 - 3t = (t - 8) \, \text{cm} $.
因为 $ BM = 4t - 32 = 4(t - 8) \, \text{cm} $,所以 $ BM = 4MN $.
综上所述,$ BM = 4MN $.
(2) 点 M,N 在运动过程中,若 $BM = 4cm$,$MN = 3cm$,直接写出 $\frac{AP}{PB}$ 的值.
$\frac{1}{7}$ 或 $\frac{5}{11}$ 或 $\frac{3}{13}$ 或 $\frac{3}{5}$