2025年启东中学作业本七年级数学上册江苏版第12页解析答案

2. 如图被称为“杨辉三角”或“贾宪三角”。图中两平行线之间的一列数：1,3,6,10,15,…,我们把第一个数记为$a_{1}$,第二个数记为$a_{2}$,第三个数记为$a_{3}$,…,第$n个数记为a_{n}$,则$a_{4}+a_{200}= $

20110

。

答案：20110 点拨: 根据题意可知 $ a _ { 1 } = 1 $, $ a _ { 2 } = 1 + 2 = 3 $, $ a _ { 3 } = 1 + 2 + 3 = 6 $, $ a _ { 4 } = 1 + 2 + 3 + 4 = 10 $, $\cdots$, 则 $ a _ { n } = 1 + 2 + 3 + \cdots + n = \frac { 1 } { 2 } n ( n + 1 ) $, 所以 $ a _ { 4 } + a _ { 200 } = 10 + \frac { 1 } { 2 } × 200 × ( 200 + 1 ) = 10 + 20100 = 20110 $.

解析：

解：由题意得，$a_{1}=1$，$a_{2}=1 + 2=3$，$a_{3}=1 + 2 + 3=6$，$a_{4}=1 + 2 + 3 + 4=10$，...，
观察可知，$a_{n}=1 + 2 + 3+\cdots +n=\frac{1}{2}n(n + 1)$，
则$a_{4}=10$，$a_{200}=\frac{1}{2}×200×(200 + 1)=\frac{1}{2}×200×201=20100$，
所以$a_{4}+a_{200}=10 + 20100=20110$。
故答案为：20110。

3. 概念学习：规定：求若干个相同的有理数(均不等于 0)的除法运算叫作除方,如$2÷2÷2$,$(-3)÷(-3)÷(-3)÷(-3)$等,类比有理数的乘方,我们把$2÷2÷2记作2^{③}$,读作“2 的圈 3 次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)^{④},读作“-3 的圈 4 次方”。一般地,把$n个a(a≠0)$相除,即$\underset{n个a}{\underbrace{a÷ a÷ a÷ … ÷ a}}$,记作

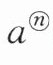
,读作“$a的圈n$次方”。
初步探究：直接写出计算结果：$2^{③}= $

$\frac { 1 } { 2 }$

,$(-\frac {1}{2})^{③}= $

-2

；
深入思考：
例如：$(-3)^{④}= (-3)÷(-3)÷(-3)÷(-3)= (-3)×(-\frac {1}{3})×(-\frac {1}{3})×(-\frac {1}{3})= (-\frac {1}{3})^{2}= (\frac {1}{3})^{2}。$
(1)试一试：仿照上面的算式,将下列运算结果直接写成幂的形式。
$5^{⑥}$=

$\left( \frac { 1 } { 5 } \right) ^ { 4 }$

,$(-\frac{1}{2})^{⑥}$=

$2 ^ { 4 }$

(2)算一算：$2^{2}÷(-\frac {1}{3})^{④}×(-2)^{③}-(-\frac {1}{3})^{⑤}÷3^{3}。$
解: $2^{2}÷(-\frac {1}{3})^{④}×(-2)^{③}-(-\frac {1}{3})^{⑤}÷3³$
$= 2^{2}÷(-3)^{2}×(-\frac {1}{2})^{1}-(-3)^{3}÷27$
$= 4×\frac {1}{9}×(-\frac {1}{2}) + 27÷27$
$= \frac {7}{9}$

答案：初步探究：$\frac { 1 } { 2 }$ -2；深入思考：(1)$\left( \frac { 1 } { 5 } \right) ^ { 4 }$ $2 ^ { 4 }$；$(2)解: 2^{2}÷(-\frac {1}{3})^{④}×(-2)^{③}-(-\frac {1}{3})^{⑤}$÷3³$= 2^{2}÷(-3)^{2}×(-\frac {1}{2})^{1}-(-3)^{3}÷27$$= 4×\frac {1}{9}×(-\frac {1}{2}) + 27÷27$$= \frac {7}{9}$.