1. 在一次数学实践活动课上,老师带领同学们探讨类似鸡蛋饼分割的问题。
(1) 在一张圆形的彩纸上,如果画 6 条直线,最多可以把这张彩纸分成多少个区域？
(2) 若将一张大饼看作一个平面,切 10 刀(每刀都是直线且切出饼的大小不要求相同),最多能把大饼切成多少块？
(3) 同学们在探讨过程中发现,直线分平面区域的规律和生活中很多场景类似。比如在一个圆形花园里,要设置若干条笔直的小径(看作直线),将花园分成不同的区域用来种植不同的花卉。若要设置 5 条小径,使花园被分成的区域最多,此时花园一共被分成了多少个区域？

2. (2024·昆山月考)【发现问题】
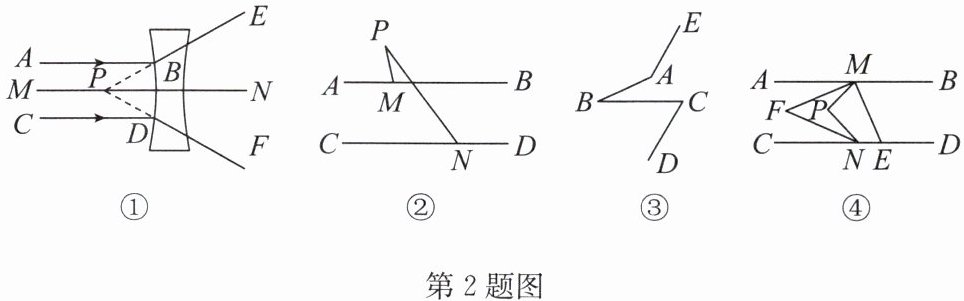
如图①,小明同学在做光的折射实验时发现：平行于主光轴 MN 的光线 AB 和 CD 经过凹透镜的折射后,折射光线 BE,DF 的反向延长线交于主光轴 MN 上一点 P.
【提出问题】
小明提出：$∠BPD$,$∠ABP和∠CDP$三个角之间存在着怎样的数量关系？
【分析问题】
已知平行,可以利用平行线的性质,把$∠BPD$分成两部分进行研究。
【解决问题】
探究一：(1)请你帮小明解决这个问题,并说明理由。
探究二：(2)如图②,$AB// CD$,则$∠P$,$∠AMP$,$∠CNP$的数量关系为______；如图③,$∠ABC= 25^{\circ }$,$∠C= 60^{\circ }$,$AE// CD$,则$∠BAE= $______$^{\circ }$。(不需要写解答过程)
利用探究一得到的结论解决下列问题：
(3)如图④,$AB// CD$,射线 ME,NF 分别平分$∠BMP和∠CNP$,ME 交直线 CD 于点 E,NF 与$∠AMP$内部的一条射线 MF 交于点 F.若$∠P= 2∠F$,求$∠FME$的度数。

(1) 解: $ \angle BPD = \angle ABP + \angle CDP $, 理由如下:
因为 $ AB // MN // CD $,
所以 $ \angle BPN = \angle ABP $, $ \angle DPN = \angle CDP $,
所以 $ \angle BPN + \angle DPN = \angle ABP + \angle CDP $,
所以 $ \angle BPD = \angle ABP + \angle CDP $。

(3) 解: 因为射线 $ ME $, $ NF $ 分别平分 $ \angle BMP $ 和 $ \angle CNP $,
所以 $ \angle PME = \frac{1}{2} \angle PMB $, $ \angle CNF = \angle PNF $,
由探究一的结论, 得 $ \angle P = \angle AMP + \angle CNP = \angle AMF + \angle PMF + \angle CNF + \angle PNF $, $ \angle F = \angle AMF + \angle CNF $。
因为 $ \angle P = 2 \angle F $, 所以 $ \angle AMF + \angle PMF + \angle CNF + \angle PNF = 2 \angle AMF + 2 \angle CNF $。
因为 $ \angle CNF = \angle PNF $, 所以 $ \angle AMF + \angle PMF = 2 \angle AMF $,
所以 $ \angle PMF = \angle AMF = \frac{1}{2} \angle AMP $,
所以 $ \angle PMF + \angle PME = \frac{1}{2} (\angle AMP + \angle PMB) $,
所以 $ \angle FME = \frac{1}{2} \angle AMB = \frac{1}{2} × 180^{\circ} = 90^{\circ} $。