1. 一节体育课$\frac{2}{3}$小时,陈老师做示范讲解用了这节课总时间的$\frac{1}{4}$。陈老师做示范讲解用了多少小时?
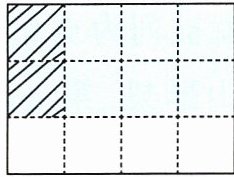
图中整个大长方形表示1小时,涂色部分表示(
一节体育课
)的时间,画斜线部分表示(
陈老师做示范讲解
)的时间。
要求陈老师做示范讲解用了多少小时,就是求(
$\frac{2}{3}$
)小时的
$\frac{1}{4}$
是多少,列式是
$\frac{2}{3}×\frac{1}{4}=\frac{1}{6}$(小时)
。
答案:一节体育课 陈老师做示范讲解 $\frac{2}{3}$ $\frac{1}{4}$ $\frac{2}{3}×\frac{1}{4}=\frac{1}{6}$(小时)
(1)$\frac{4}{7}×\frac{3}{5}=\frac{(
4
)×(
3
)}{(
7
)×(
5
)}=\frac{(
12
)}{(
35
)}$
(2)$\frac{5}{4}×\frac{7}{9}=\frac{(
5
)×(
7
)}{(
4
)×(
9
)}=\frac{(
35
)}{(
36
)}$
答案:(1)$\frac{4}{7}×\frac{3}{5}=\frac{(4)×(3)}{(7)×(5)}=\frac{(12)}{(35)}$
(2)$\frac{5}{4}×\frac{7}{9}=\frac{(5)×(7)}{(4)×(9)}=\frac{(35)}{(36)}$
3. 计算下列各题。
$\frac{7}{9}×\frac{2}{3}=$ $\frac{9}{10}×\frac{3}{4}=$
$\frac{5}{8}×\frac{1}{6}=$ $\frac{2}{7}×\frac{4}{5}=$
$\frac{4}{51}×\frac{17}{16}=$ $\frac{18}{35}×\frac{85}{48}=$
答案:$\frac{14}{27}$ $\frac{27}{40}$ $\frac{5}{48}$ $\frac{8}{35}$ $\frac{1}{12}$ $\frac{51}{56}$
[点拨]计算时,注意将结果化为最简分数。
4. 算一算,比一比,填一填。
$\frac{9}{10}×\frac{4}{5}$
<
$\frac{9}{10}$ $\frac{7}{6}×\frac{4}{7}$
<
$\frac{7}{6}$
$\frac{9}{10}×1$
=
$\frac{9}{10}$ $\frac{7}{6}×1$
=
$\frac{7}{6}$
$\frac{9}{10}×\frac{6}{5}$
>
$\frac{9}{10}$ $\frac{7}{6}×\frac{8}{7}$
>
$\frac{7}{6}$
我发现:一个分数乘小于1的数,积比原分数(
小
);一个分数乘1,积(
等于
)原分数;一个分数乘大于1的数,积比原分数(
大
)。
根据上面的规律比大小:
$\frac{7}{8}×\frac{5}{9}$
<
$\frac{7}{8}$ $\frac{13}{8}×\frac{5}{6}$
>
$\frac{5}{6}$
答案:(竖排)< = > < = > 小 等于 大 < >
[点拨]可以先计算出结果,再比较大小,也可以根据分数乘分数的意义比较大小,最后总结规律即可。
5. 毛竹是世界上生长速度最快的植物。在生长期,一种毛竹每小时可以长高$\frac{24}{5}$厘米。照这样计算,这种毛竹$\frac{1}{6}$小时可以长高多少厘米?一天呢?
答案:$\frac{1}{6}×\frac{24}{5}=\frac{4}{5}$(厘米)
$24×\frac{24}{5}=\frac{576}{5}$(厘米)=115$\frac{1}{5}$(厘米)
答:这种毛竹$\frac{1}{6}$小时可以长高$\frac{4}{5}$厘米,一天可以长高115$\frac{1}{5}$厘米。
[点拨]已知毛竹每小时可以长高$\frac{24}{5}$厘米,求$\frac{1}{6}$小时可以长高多少厘米,用乘法计算。求一天可以长高多少厘米,用乘法计算,注意一天要换成24小时再计算。
6. 一小袋面粉重$\frac{5}{2}$千克,第一天用去这袋面粉的$\frac{1}{5}$,第二天用去了$\frac{1}{4}$千克,哪一天用去的多?
提示:注意$\frac{1}{5}$和$\frac{1}{4}$千克表示的意义不同哟!
答案:$\frac{5}{2}×\frac{1}{5}=\frac{1}{2}$(千克) $\frac{1}{2}>\frac{1}{4}$
答:第一天用去的多。
[点拨]先求出第一天用去多少千克,再与第二天用去的质量进行比较。
7. 如图,把一个大三角形三条边上的中点连接起来,可以得到一个小三角形,再把小三角形三条边上的中点连接起来,又可以得到一个更小的三角形(图中涂色部分)。如果大三角形的面积是$\frac{16}{5}$平方厘米,那么涂色部分的面积是( )平方厘米。

答案:$\frac{1}{5}$ [点拨]如图,把大三角形平均分成16份,涂色部分占其中的1份,则涂色部分的面积是大三角形面积的$\frac{1}{16}$,即$\frac{16}{5}×\frac{1}{16}=\frac{1}{5}$(平方厘米)。
